大数の弱法則

解説

大数の弱法則とは，たくさんの試行を平均すると，本当の平均（母平均）に近づく という性質です．
たとえばサイコロを何度も振って出た目の平均をとると，回数を増やすほど理論上の平均 3.5 に近づきます．
つまり「偶然のブレ」は試行回数が多いほど平均で打ち消される，という直感を数学的に示した定理です．

定義

大数の弱法則（Weak Law of Large Numbers）

独立同分布な確率変数列 $X_1,X_2,\dots ,X_n$ が存在し，
それぞれの期待値が $\mathbb{E}[X_i]=\mu$，分散が $\mathrm{V}[X_i]={\sigma }^2<\mathrm{\infty }$ であるとする．
このとき，標本平均

$${\overline{X}}_n=\frac{1}{n}\sum _{i=1}^n{X}_i$$

は確率的に母平均 $\mu$ に収束する．すなわち

$$\mathrm{\forall }\epsilon >0,\underset{n\to \mathrm{\infty }}{lim}Pr(|{\overline{X}}_n-\mu |\ge \epsilon )=0.$$

これを 確率収束 と呼び，

$${\overline{X}}_n\stackrel{p}{\to }\mu$$

と書く．

注意

大数の弱法則は，各確率変数が 期待値と分散をもつ ことを仮定しています .
これが成立しない場合，標本平均が母平均に確率収束するとは限りません.

大数の弱法則の証明

解説

大数の弱法則は定義の左辺から類推できるように チェビシェフの不等式 から証明できます.

チェビシェフの不等式

---

チェビシェフの不等式の証明

証明

独立同分布 $X_1,\dots ,X_n$ に対し，$\mathbb{E}[X_i]=\mu$，$\mathrm{V}[X_i]={\sigma }^2<\mathrm{\infty }$ とする．
標本平均 ${\overline{X}}_n=\frac{1}{n}\sum _{i=1}^n{X}_i$ の期待値と分散は

$$\mathbb{E}[{\overline{X}}_n]=\mu ,\mathrm{V}[{\overline{X}}_n]=\frac{{\sigma }^2}{n}.$$

チェビシェフの不等式より任意の $\epsilon >0$ について

$$Pr(|{\overline{X}}_n-\mu |\ge \epsilon )\le \frac{\mathrm{V}[{\overline{X}}_n]}{{\epsilon }^2}=\frac{{\sigma }^2}{n{\epsilon }^2}\underset{n\to \mathrm{\infty }}{\overset{}{\to }}0.$$

よって ${\overline{X}}_n\stackrel{p}{\to }\mu$．これが大数の弱法則．

シミュレーションで確認

先ほど説明したように期待値が存在しない場合大数の弱法則は成立しません.
これをシミュレーションで確認してみましょう.

$t$ 分布は自由度2のとき期待値が$0$ですが、自由度が1のとき(コーシー分布)では期待値が存在しません.

t分布

---

PDF・CDF・期待値・分散

t分布の確率密度関数

確率密度関数

$$\begin{array}{rl}f(t;1)& =\frac{1}{\pi (1+t^2)}\\ f(t;2)& ={(2+t^2)}^{-\frac{3}{2}}\end{array}$$

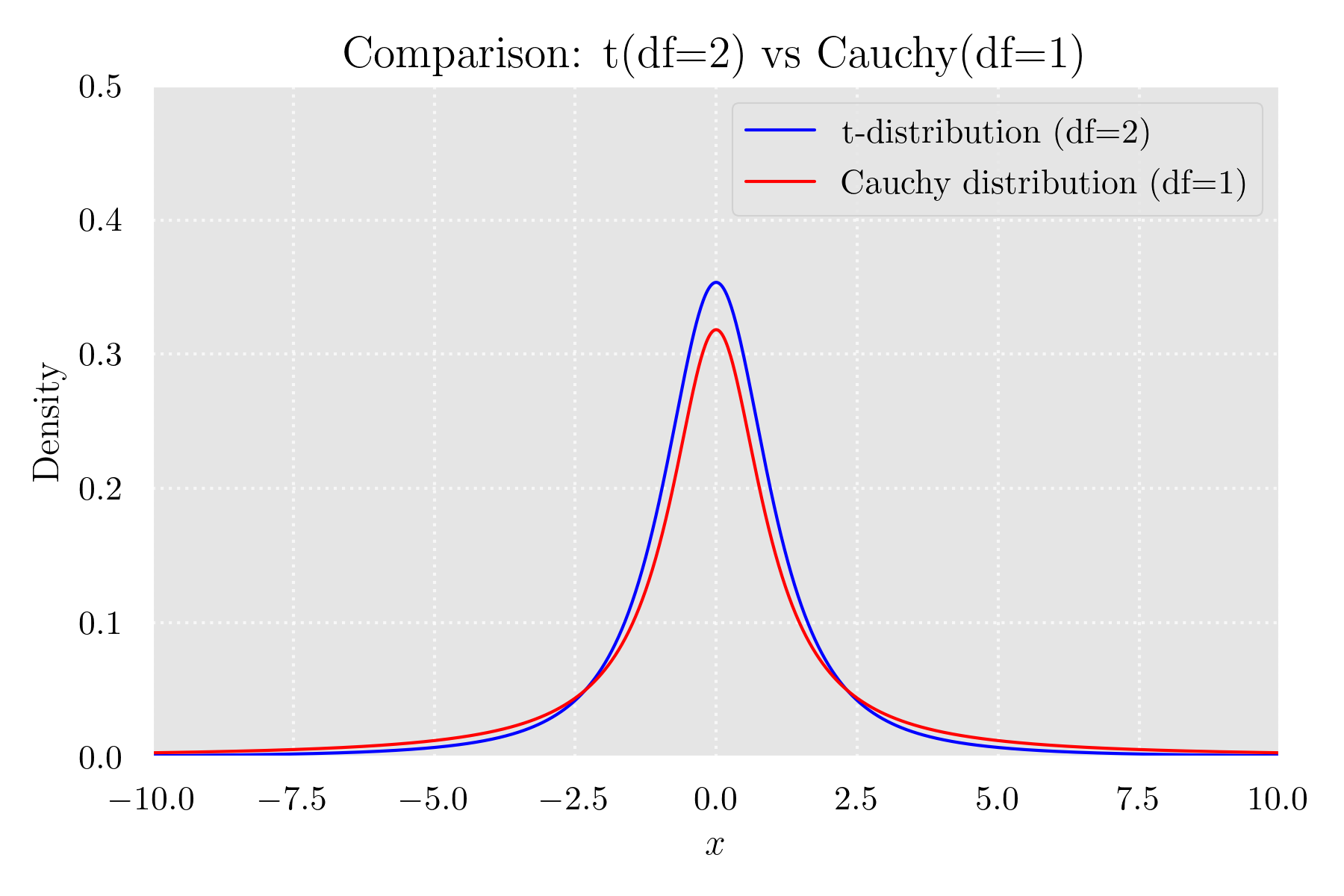
シミュレーション

横軸にそれぞれの分布からのサンプル数, 縦軸にそのサンプルの平均をとります.

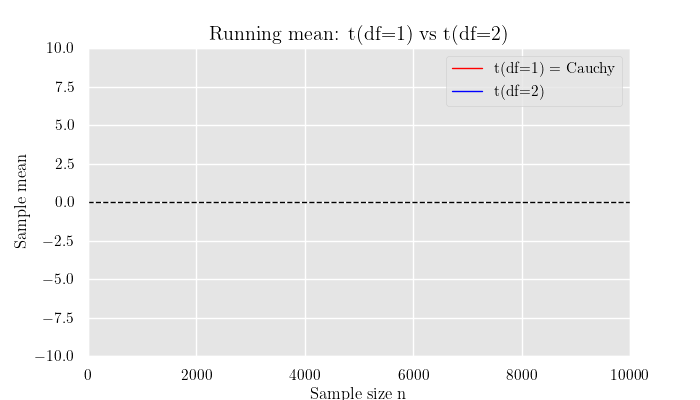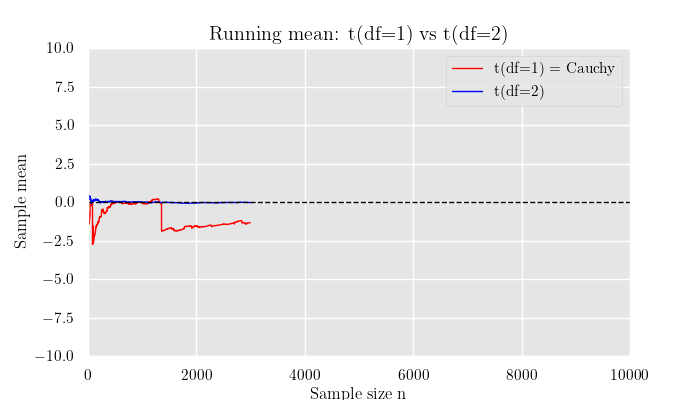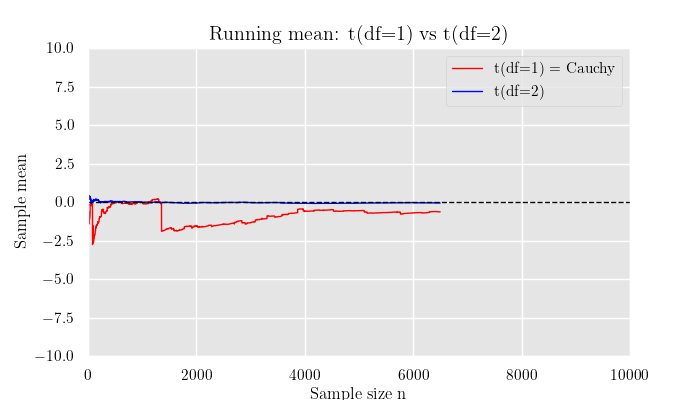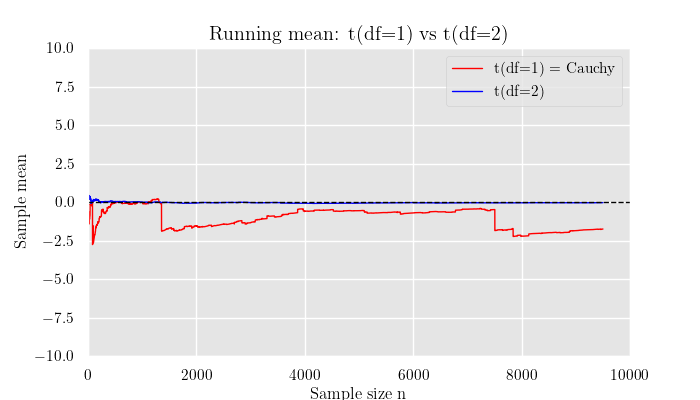
解説

シミュレーションの結果から，期待値が存在しない分布では標本平均が安定せず収束していない ことが確認できます．
コーシー分布（自由度1）は裾が非常に重く，まれに極端に大きな値が出現するため，平均値が収束しません．
そのためサンプルを増やしても平均が一定値に近づかず，グラフ上でも大きく揺れ動いたままになります．

一方で，$t$ 分布（自由度2）は期待値が $0$ で存在するため，サンプル数を増やすにつれて平均が $0$ に収束していきます．

参考文献

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る