チェビシェフの不等式

Takeda Katsuji2025/10/26約2分

定義

チェビシェフの不等式（Chebyshev’s inequality）
平均 $μ = E [X]$ と分散 $σ^{2} = V [X]$ をもつ確率変数 $X$ と任意の $a > 0$ に対して

Pr (| X - μ | \geq a) \leq \frac{σ^{2}}{a^{2}} .

特に $a = k σ (k > 0)$ とおくと

Pr (| X - μ | \geq k σ) \leq \frac{1}{k^{2}} .

チェビシェフの不等式の証明

解説

チェビシェフの不等式は 平均値(期待値)から $k σ$ 以上ずれる確率は高々 $\frac{1}{k^{2}}$ を表す不等式です.

期待値と分散がわかっていれば確率変数 $X$ の分布がわからなくても上から抑えることができます.

証明はマルコフの不等式から簡単に導けます.

証明

マルコフの不等式より，非負の確率変数 $Y \geq 0$ と $t > 0$ に対して

Pr (Y \geq t) \leq \frac{E [Y]}{t} .

ここで確率変数 $X$ の平均と分散を

μ = E [X], σ^{2} = V [X]

とおく．

$Y = (X - μ)^{2} \geq 0$ とし， $t = a^{2} (a > 0)$ を代入すると，

Pr ((X - μ)^{2} \geq a^{2}) \leq \frac{E [(X - μ)^{2}]}{a^{2}} = \frac{σ^{2}}{a^{2}} .

左辺は $Pr (| X - μ | \geq a)$ なので，

Pr (| X - μ | \geq a) \leq \frac{σ^{2}}{a^{2}} .

これが チェビシェフの不等式 である．

また別形式で $a = k σ$ とおくと,

\begin{array}{r} Pr (| X - μ | \geq k σ) \leq \frac{1}{k^{2}} . \end{array}

令和5年度の共通テスト数学Ⅱ・Bの点数分布をし使用してチェビシェフの不等式を確認します.

総受験者数	平均	標準偏差
316728	61.48	20.18

横軸に得点、縦軸にその得点の人数のヒストグラム

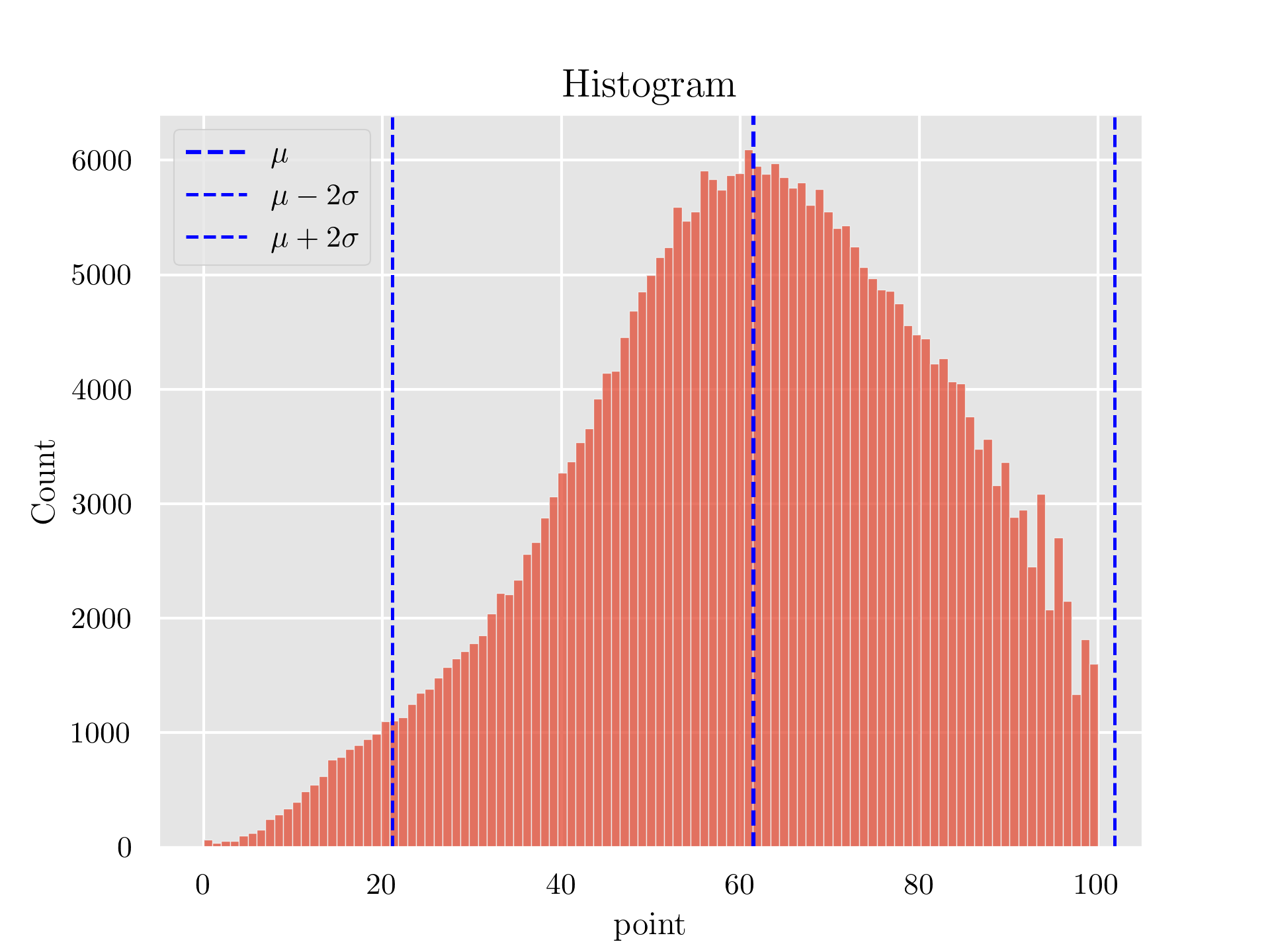
チェビシェフの不等式より, 平均値から $2 σ$ 以上離れる確率は $\frac{1}{4}$ つまり $25$ %以下

今回使用するデータでは,

点数の上限は100点のため101.8点以上の得点者は0人, 21.13点以下の人数は10971人なので全体の3.46%

マルコフの不等式同様に粗い抑え方であることがわかります.