![日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]](https://m.media-amazon.com/images/I/61GHu8G0tgL._SY425_.jpg)
日本統計学会
過去問2012年・2013年
解答
確率変数 の累積分布関数を とする.
これは区間 の一様分布の累積分布関数であるため, は 区間 の一様分布に従う.
この問題のように連続な累積分布関数をもつ確率変数について, 累積分布関数で変数変換することを 確率積分変換 といいます. また確率積分変換した確率変数は区間 の一様分布に従います.
この大問の山場と言える問題で順序統計量の基本が詰まっています。
解説
確率変数列の最小値、最大値、中央値を次のように表します.
- 最小値:
- 中央値:
- 最大値:
解答
最大値 の累積分布関数を とする.
という事象は がすべて 以下という事象と同値 であるため,
が互いに独立であることを用いて,
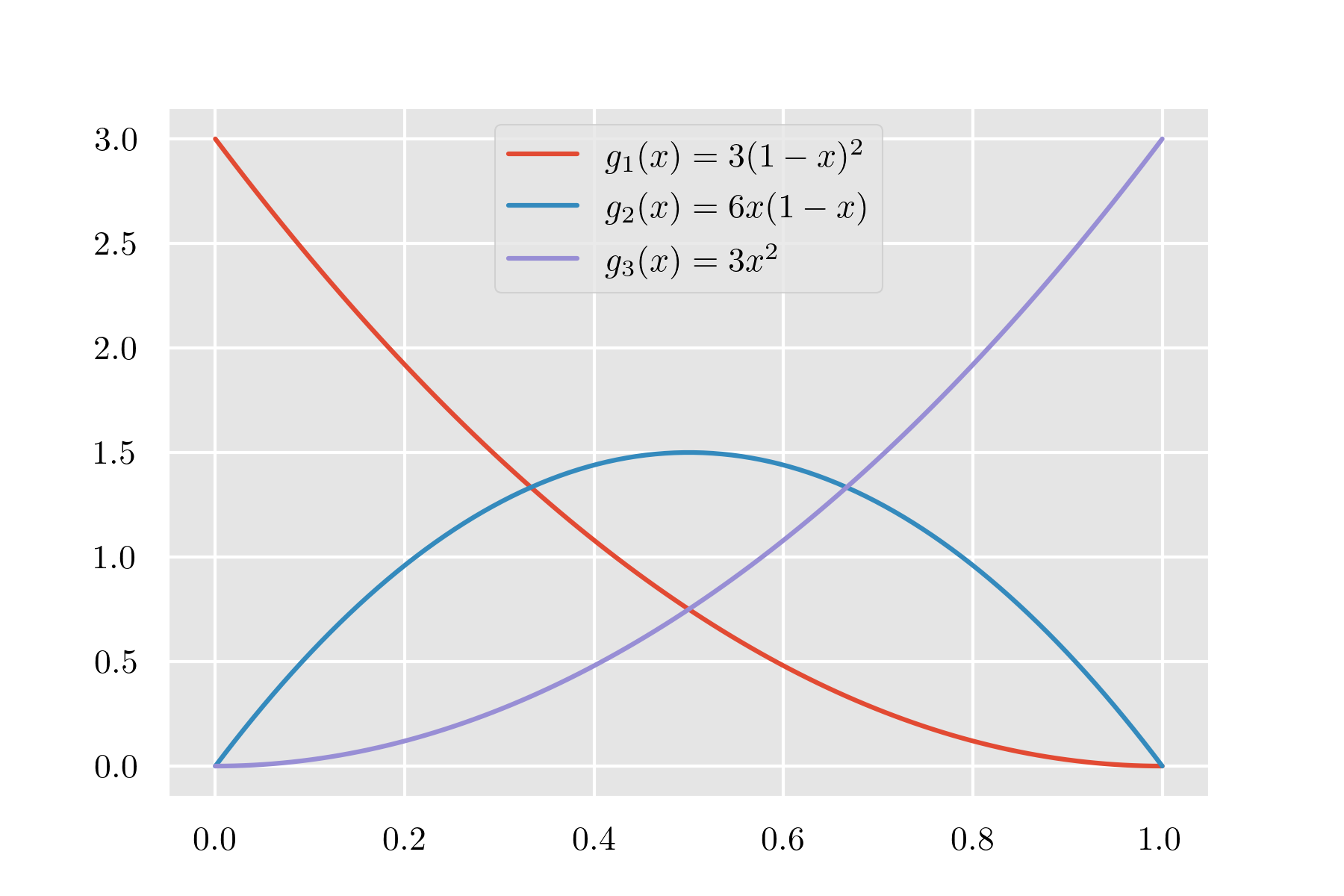
したがって確率密度関数は
最小値 の累積分布関数を とする.
という事象は がすべて より大きいという事象と同値 であるため,
が互いに独立であることを用いて,
よって
したがって確率密度関数は
中央値 の累積分布関数を とする.
という事象は 少なくとも2個以上が より大きいという事象と同値 であるため,
以下の二通りが考えられる.
- のうち二つが 以上
- すべてが 以上
二つの事象は互いに排反であるため は,
したがって と確率密度関数 は,
![日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]](https://m.media-amazon.com/images/I/61GHu8G0tgL._SY425_.jpg)
日本統計学会
過去問2012年・2013年

日本統計学会
統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

竹村 彰通
統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

![日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]](https://m.media-amazon.com/images/I/61GHu8G0tgL._SY425_.jpg)
![日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]](https://m.media-amazon.com/images/I/61GHu8G0tgL._SY425_.jpg)


