カイ二乗分布の性質

定義

カイ二乗分布は独立に標準正規分布に従う確率変数の二乗の和が従う分布です.

つまり $Z_i\stackrel{i.i.d.}{\sim }\mathcal{N}(0,1)$ のとき,

$$\begin{array}{r}X=\sum _{i=1}^n{Z}_i^2\sim {\chi }^2(n)\end{array}$$

統計量 $X$ は自由度 $n$ のカイ二乗分布に従います.

カイ二乗分布は様々な性質・関係が学べる分布 であり, 以下の表ように他分布と関連しています.

確率分布	関係	式
カイ二乗分布	標準正規分布の二乗和	$X=\sum _{i=1}^n{Z}_i^2,Z_i\sim \mathcal{N}(0,1)$
t分布	標準正規分布とカイ二乗分布の比	$T={\displaystyle \frac{Z}{\sqrt{X/n}}},Z\sim \mathcal{N}(0,1),X\sim {\chi }^2(n)$
F分布	カイ二乗分布の比	$F={\displaystyle \frac{X_1/d_1}{X_2/d_2}},X_1\sim {\chi }^2(d_1),X_2\sim {\chi }^2(d_2)$

他にもベータ関数・ガンマ関数, 変数変換, 再生性など統計検定で重要な性質の宝庫です.

1. 確率密度関数

定義

自由度 $n$ , $x>0$ に対して

$$\begin{array}{r}f(x)=\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{x}^{\frac{n}{2}-1}{e}^{-\frac{x}{2}}\end{array}$$

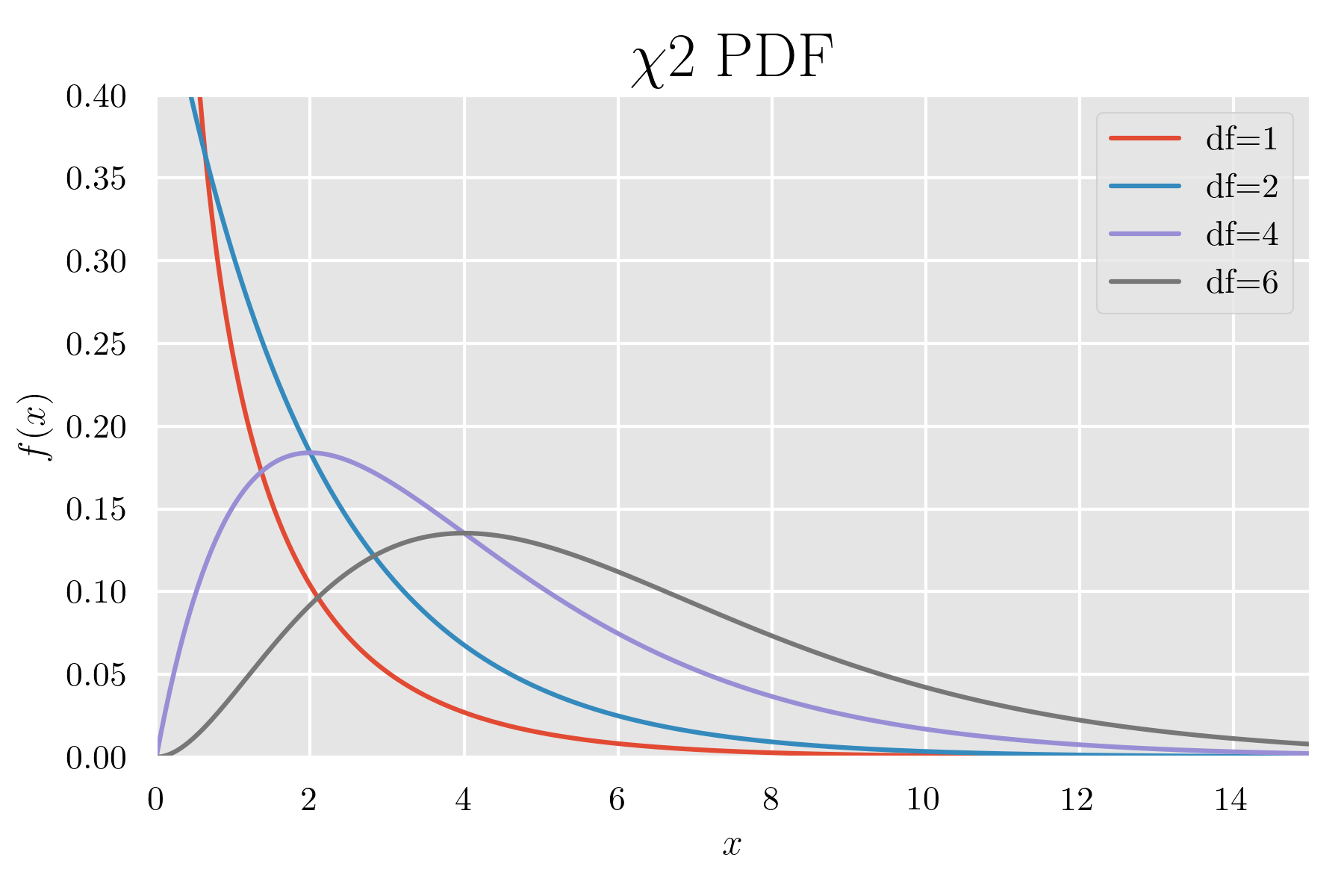
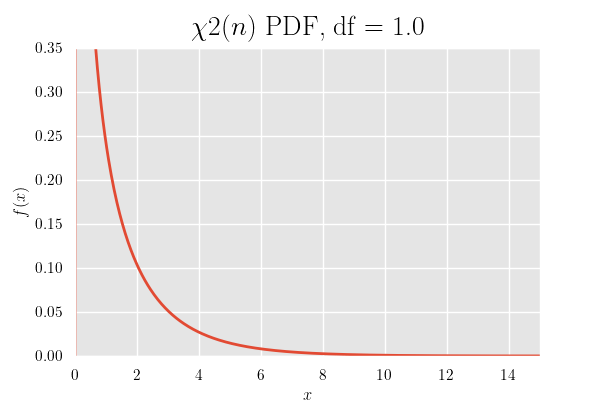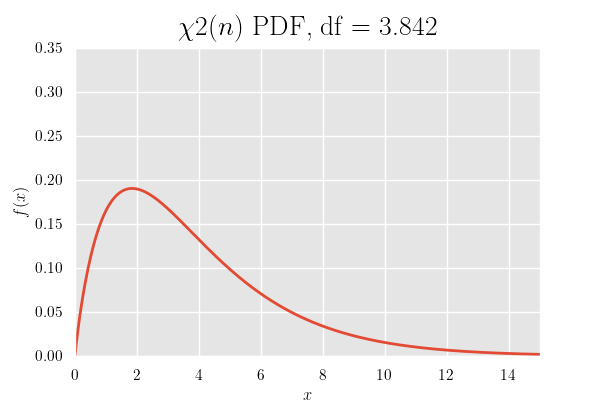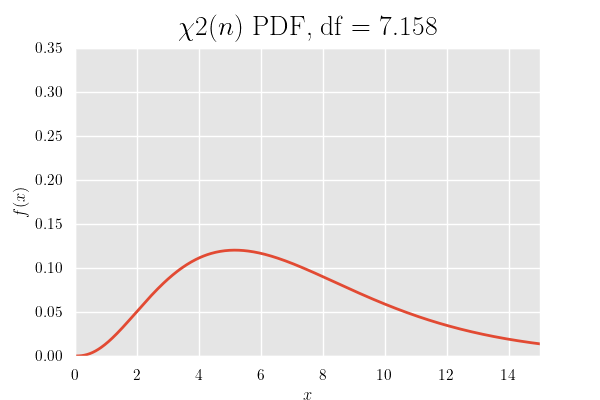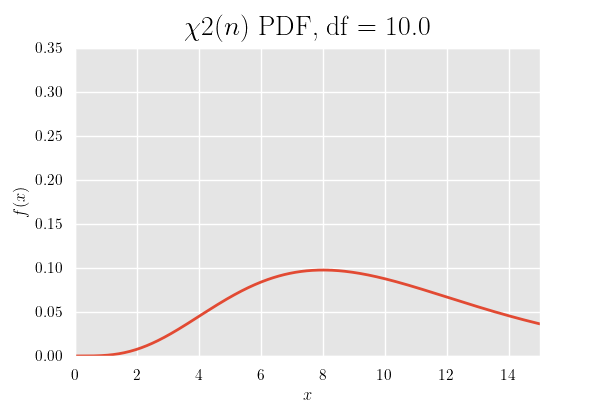
確率密度関数のグラフ

カイ二乗分布の確率密度関数は定義域が0以上で 自由度が大きくなるにつれて山が右にシフト していきます.

確率密度関数の導出には2種類あります.

• 標準正規分布の二乗和の定義から導出
• ガンマ分布の再生性から導出

両方ともなかなか歯ごたえのある導出になるので別記事で紹介することとします.

2. 累積分布関数

定義

累積分布関数は不完全ガンマ関数(ガンマ積分の不定積分)で表します.

第１種不完全ガンマ関数 $\gamma (a,x)$

$$\begin{array}{r}\gamma (a,x)={\int }_0^x{t}^{a-1}{e}^{-t}dt\end{array}$$

を用いて.

$$\begin{array}{rl}F(x)& =\frac{\gamma (\frac{n}{2},\frac{x}{2})}{\mathrm{\Gamma }(\frac{n}{2})}\end{array}$$

と表せる.

導出の手順はこちら

導出

$$\begin{array}{rl}f(u)& =\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{u}^{\frac{n}{2}-1}{e}^{-\frac{u}{2}}\\ F(x)& ={\int }_0^{x}f(u)du\\ & =\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^x{u}^{\frac{n}{2}-1}{e}^{-\frac{u}{2}}du\end{array}$$

$u=2t$ で置換積分を行う.

$$\begin{array}{rl}F(x)& =\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^{x/2}(2t{)}^{\frac{n}{2}-1}{e}^{-t}2dt\\ & =\frac{\gamma (\frac{n}{2},\frac{x}{2})}{\mathrm{\Gamma }(\frac{n}{2})}\end{array}$$

3. 期待値

期待値

$$\mathbb{E}[X]=n$$

導出の手順はこちら

導出

自由度 $n$ のカイ二乗分布 $X\sim {\chi }^2(n)$ の密度は

$$f(x)=\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{x}^{\frac{n}{2}-1}{e}^{-x/2}(x>0)$$

であるから，

$$\begin{array}{rl}\mathbb{E}[X]& ={\int }_0^{\mathrm{\infty }}xf(x)dx\\ & =\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{x}^{\frac{n}{2}}{e}^{-x/2}dx\end{array}$$

ここで $x=2t$ とおくと $dx=2dt$，

$$\begin{array}{rl}\mathbb{E}[X]& =\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}(2t{)}^{\frac{n}{2}}{e}^{-t}2dt\\ & =\frac{2^{\frac{n}{2}+1}}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{t}^{\frac{n}{2}}{e}^{-t}dt\\ & =\frac{2\mathrm{\Gamma }(\frac{n}{2}+1)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}=2\cdot \frac{n}{2}=n\end{array}$$

別視点（ガンマ分布）

${\chi }^2(n)$ は $\mathrm{Gamma}(\alpha =\frac{n}{2},\theta =2)$ に等価であり，ガンマ分布の期待値 $\mathbb{E}[X]=\alpha \theta$ からも $n$ が得られる.

4. 分散

分散

$$\mathrm{V}[X]=2n$$

導出の手順はこちら

導出

自由度 $n$ のカイ二乗分布 $X\sim {\chi }^2(n)$ の密度

$$f(x)=\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{x}^{\frac{n}{2}-1}{e}^{-x/2}(x>0)$$

より

$$\mathbb{E}[X^2]=\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{x}^{\frac{n}{2}+1}{e}^{-x/2}dx.$$

$x=2t$ とおくと $dx=2dt$ だから

$$\begin{array}{rl}\mathbb{E}[X^2]& =\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}(2t{)}^{\frac{n}{2}+1}{e}^{-t}2dt\\ & =\frac{2^{\frac{n}{2}+2}}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{t}^{\frac{n}{2}+1}{e}^{-t}dt\\ & =\frac{4\mathrm{\Gamma }(\frac{n}{2}+2)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}=4(\frac{n}{2}+1)\frac{n}{2}=n(n+2).\end{array}$$

よって

$$\mathrm{V}[X]=\mathbb{E}[X^2]-\{\mathbb{E}[X]{\}}^2=n(n+2)-n^2=2n.$$

別視点（ガンマ分布）

${\chi }^2(n)\equiv \mathrm{Gamma}(\alpha =\frac{n}{2},\theta =2)$ なので $\mathrm{V}[X]=\alpha {\theta }^2=(\frac{n}{2})\cdot 4=2n$ でも得られる.

5. 積率母関数

積率母関数

$$M_X(t)=(1-2t{)}^{-\frac{n}{2}}(t<\frac{1}{2})$$

導出の手順はこちら

導出

自由度 $n$ のカイ二乗分布 $X\sim {\chi }^2(n)$ の密度

$$f(x)=\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{x}^{\frac{n}{2}-1}{e}^{-x/2}(x>0)$$

から

$$\begin{array}{rl}{M}_X(t)& ={\int }_0^{\mathrm{\infty }}{e}^{tx}f(x)dx\\ & =\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^{\mathrm{\infty }}{x}^{\frac{n}{2}-1}{e}^{-(\frac{1}{2}-t)x}dx\end{array}$$

置換 $u=(1-2t)x(t<\frac{1}{2})$ を用いると，$x={\displaystyle \frac{u}{1-2t}},dx={\displaystyle \frac{du}{1-2t}}$ なので

$$\begin{array}{rl}{M}_X(t)& =\frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^{\mathrm{\infty }}(\frac{u}{1-2t}{)}^{\frac{n}{2}-1}{e}^{-u/2}\frac{du}{1-2t}\\ & =\frac{1}{(1-2t{)}^{n/2}}\cdot \frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^{\mathrm{\infty }}{u}^{\frac{n}{2}-1}{e}^{-u/2}du\\ & =\frac{1}{(1-2t{)}^{n/2}}\cdot \frac{1}{2^{n/2}\mathrm{\Gamma }(\frac{n}{2})}{2}^{n/2}\mathrm{\Gamma }(\frac{n}{2})\\ & =(1-2t{)}^{-n/2}.\end{array}$$

ゆえに

$$M_X(t)=(1-2t{)}^{-\frac{n}{2}}(t<\frac{1}{2}).$$

チェック（平均と分散）

$$M_X^{\prime }(0)=n,M_X^{″}(0)-\{M_X^{\prime }(0){\}}^2=2n.$$

6. 再生性

定義

再生性は積率母関数を使うと簡単に証明できます.
確率変数 $X,Y$は独立に自由度 $n,m$ のカイ二乗分布に従うとき,

$$\begin{array}{r}X\sim \chi 2(n),Y\sim \chi 2(m)\end{array}$$

$Z=X+Y$, それぞれの積率母関数 $M_X(t),M_Y(t),M_Z(t)$ として
積率母関数の性質より $X,Y$ が独立のとき

$$\begin{array}{rl}{M}_Z(t)& =M_X(t)\cdot M_Y(t)\\ & ={(1-2t)}^{-\frac{n}{2}}\cdot {(1-2t)}^{-\frac{m}{2}}\\ & ={(1-2t)}^{-\frac{n+m}{2}}\end{array}$$

これは自由度 $n+m$ のカイ二乗分布の積率母関数であり, 積率母関数の一意性から,

$$\begin{array}{r}Z\sim \chi 2(n+m)\end{array}$$

同様に $m$ 個の独立な $\chi 2(k_i)$ の和も $\chi 2\left(\sum _{i=1}^m{k}_i\right)$ に従う.

参考文献

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る