二項分布の性質

Takeda Katsuji2025/09/25約3分

二項分布の性質

解説

二項分布は試行回数 $n$ 、成功確率を $p$ とする独立ベルヌーイ試行の和で表されます.
これは成功回数の分布であり、回数(カウント)の分布をモデル化するときに頻繁に利用されます.

独立同分布のベルヌーイ分布に従う確率変数 $I_{i}$ とする.
二項分布は

\begin{aligned} I_{i} & \overset{i . i . d .}{\sim} Bern (p) \\ X & = \sum_{i}^{n} I_{i} \sim B i n (n, p) \end{aligned}

で表される.

1. 確率質量関数

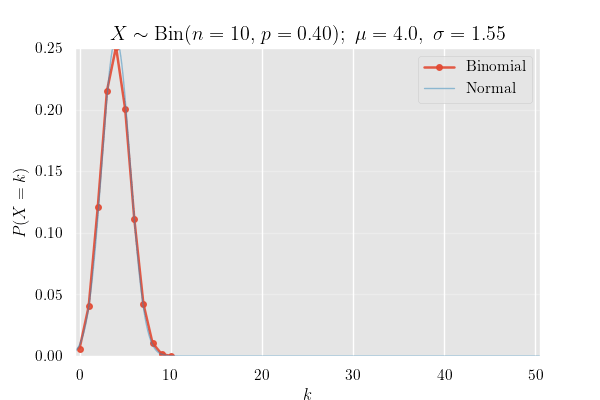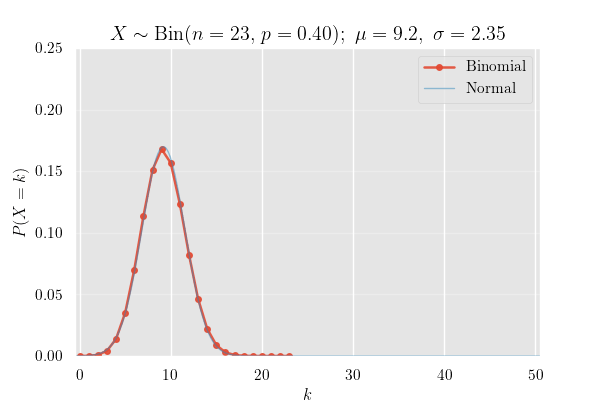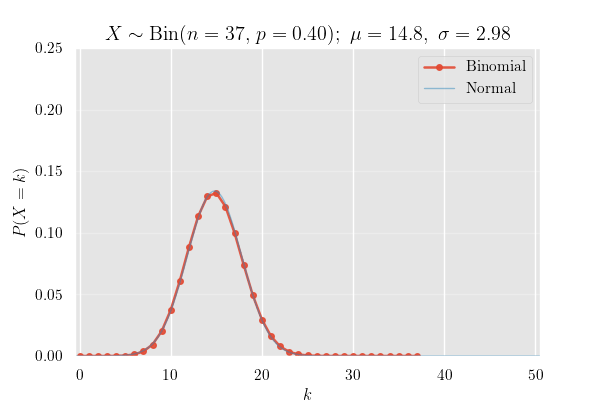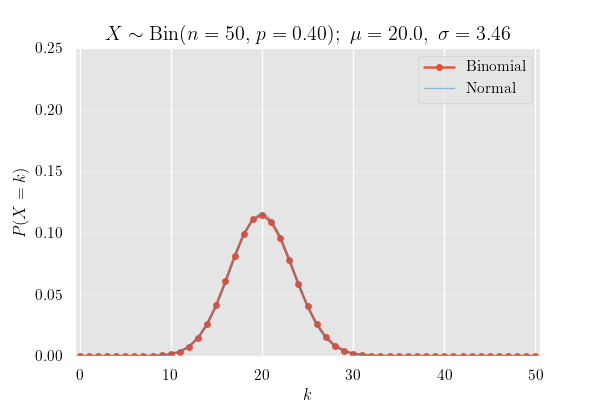
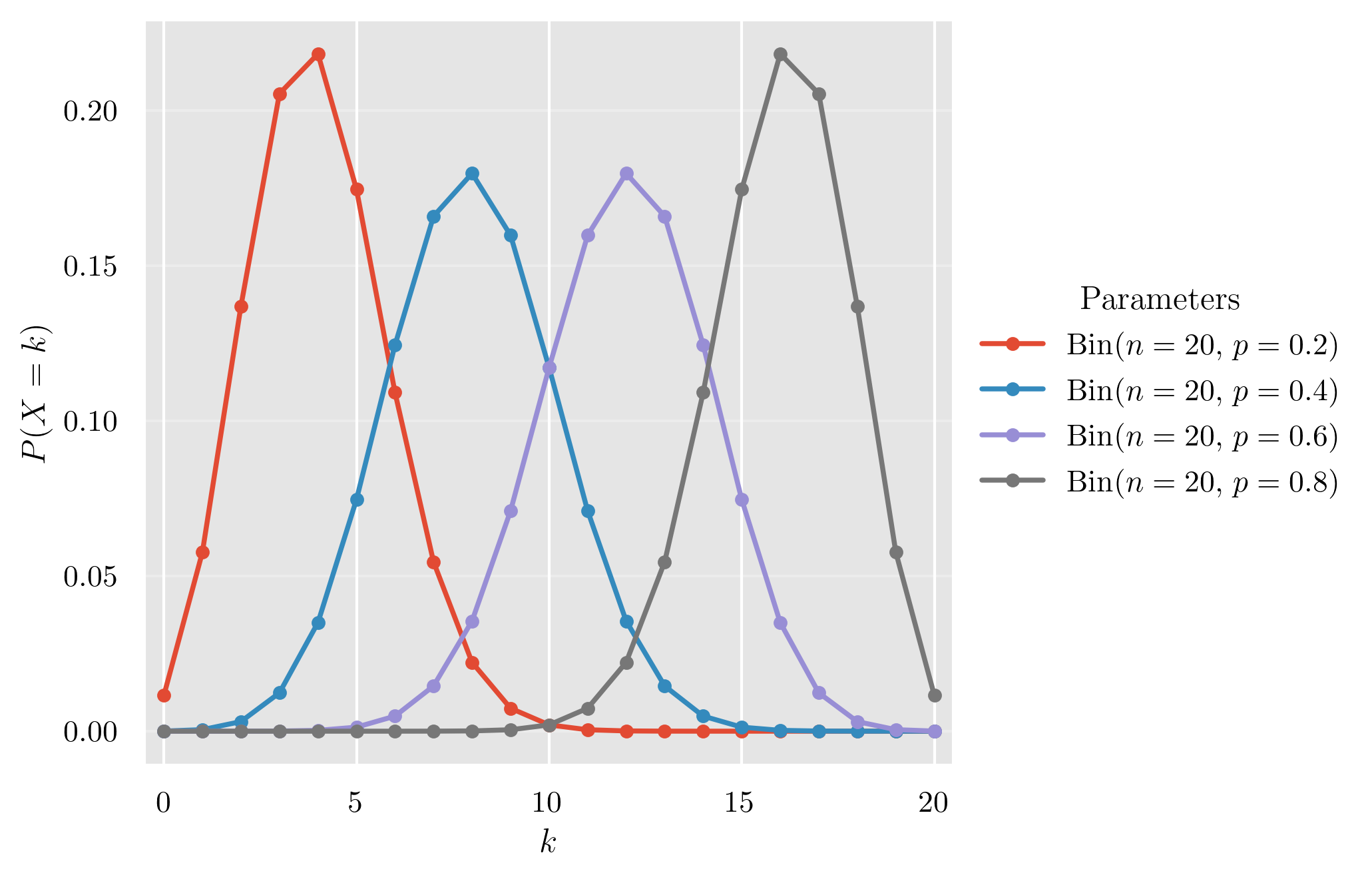
確率質量関数 (PMF)

P (X = k) =_{n} C_{k} p^{k} (1 - p)^{n - k}, k = 0, 1, \dots, n .

確率質量関数のグラフ

2. 累積分布関数

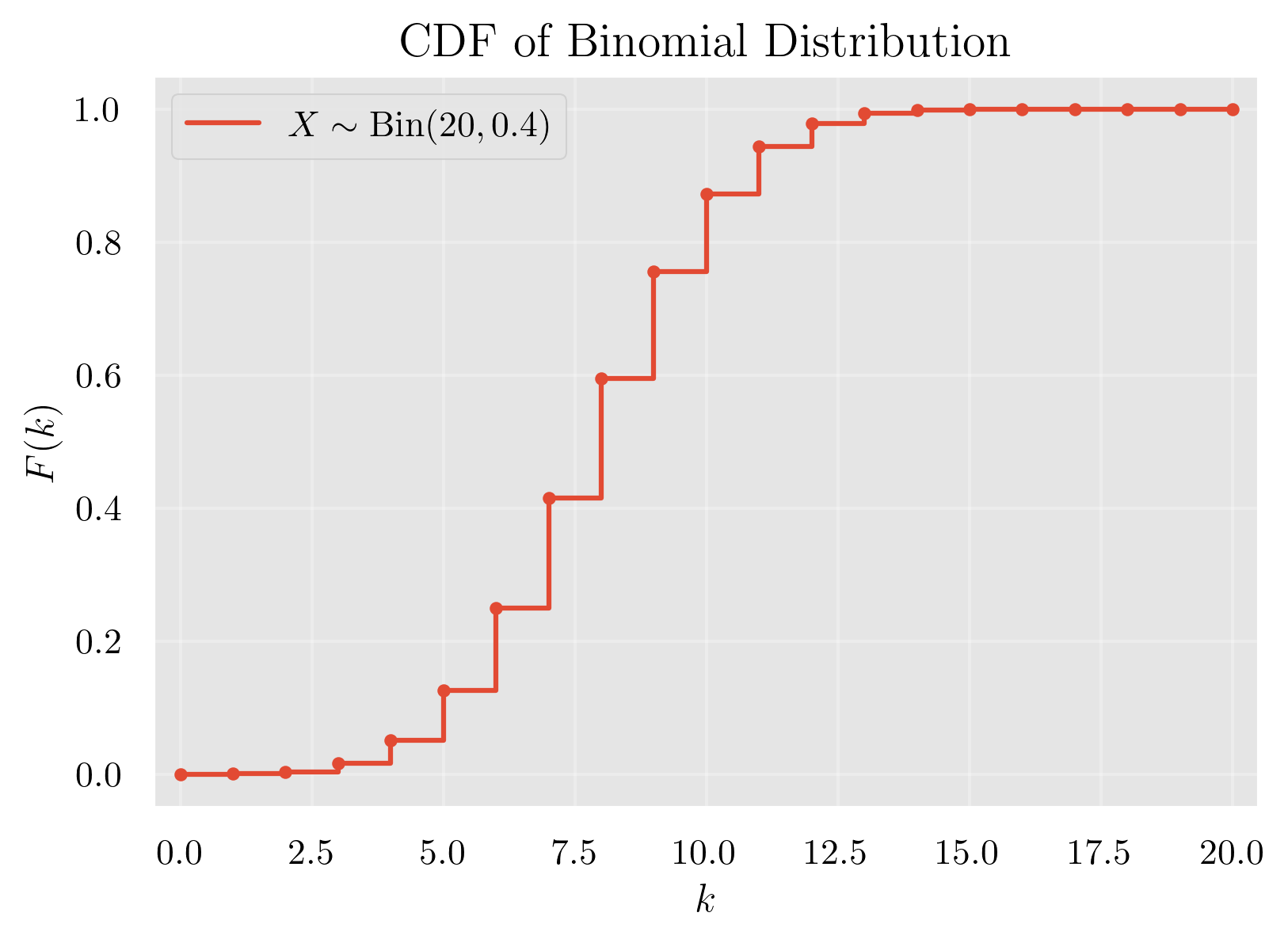
累積分布関数 (CDF)

F (k) = P (X \leq k) = \sum_{j = 0}^{⌊ k ⌋} (\binom{n}{j}) p^{j} (1 - p)^{n - j} .

累積分布関数のグラフ

3. 期待値

期待値

E [X] = n p .

導出の手順はこちら　ベルヌーイ分布から

導出

X = \sum_{i = 1}^{n} I_{i}, I_{i} \overset{i . i . d .}{\sim} Bernoulli (p) .

\begin{aligned} E [X] & = \sum_{i = 1}^{n} E [I_{i}] \\ = \sum_{i = 1}^{n} p \\ = n p . \end{aligned}

導出の手順はこちら確率質量関数から

導出

二項分布 $X \sim Bin (n, p)$ に対して

E [X] = \sum_{k = 0}^{n} k_{n} C_{k} p^{k} (1 - p)^{n - k} .

$_{n} C_{k}$ を階乗で展開し， $k$ と約分する:

\begin{aligned} k_{n} C_{k} & = k \cdot \frac{n!}{k! (n - k)!} \\ = \frac{k}{k!} \cdot \frac{n!}{(n - k)!} = \frac{1}{(k - 1)!} \cdot \frac{n!}{(n - k)!} \\ = \frac{n (n - 1)!}{(k - 1)! (n - k)!} = n \cdot \frac{(n - 1)!}{(k - 1)! {(n - 1) - (k - 1)}!} \\ = n \cdot_{n - 1} C_{k - 1} . \end{aligned}

これを元の和に代入し， $m = k - 1$ と置換する:

\begin{aligned} E [X] & = \sum_{k = 1}^{n} n_{n - 1} C_{k - 1} p^{k} (1 - p)^{n - k} \\ = n p \sum_{k = 1}^{n}_{n - 1} C_{k - 1} p^{k - 1} (1 - p)^{(n - 1) - (k - 1)} \\ = n p \sum_{m = 0}^{n - 1}_{n - 1} C_{m} p^{m} (1 - p)^{(n - 1) - m} . \end{aligned}

ここで $\sum_{m = 0}^{n - 1}_{n - 1} C_{m} p^{m} (1 - p)^{(n - 1) - m} = 1$ （全確率）なので

E [X] = n p \cdot 1 = n p .

4. 分散

分散

V [X] = n p (1 - p) .

導出の手順はこちらベルヌーイ分布から

導出

独立より $Cov [I_{i}, I_{j}] = 0 (i \neq j)$ 、かつ $V [I_{i}] = p (1 - p)$ .

V [X] = \sum_{i = 1}^{n} V [I_{i}] = n p (1 - p) .

導出の手順はこちら確率質量関数から

導出

$X \sim Bin (n, p)$ の分散は

V [X] = E [X^{2}] - E [X]^{2} .

ここでは $E [X (X - 1)]$ を先に求めてから
$E [X^{2}] = E [X (X - 1)] + E [X]$ を用いる.

まず二階階乗モーメント:

\begin{aligned} E [X (X - 1)] & = \sum_{k = 0}^{n} k (k - 1)_{n} C_{k} p^{k} (1 - p)^{n - k} . \end{aligned}

$_{n} C_{k}$ を階乗で展開し約分する:

\begin{aligned} k (k - 1)_{n} C_{k} & = k (k - 1) \cdot \frac{n!}{k! (n - k)!} \\ = \frac{k (k - 1)}{k!} \cdot \frac{n!}{(n - k)!} = \frac{1}{(k - 2)!} \cdot \frac{n!}{(n - k)!} \\ = \frac{n (n - 1) (n - 2)!}{(k - 2)! (n - k)!} \\ = n (n - 1) \cdot_{n - 2} C_{k - 2} . \end{aligned}

代入し， $m = k - 2$ と置換する:

\begin{aligned} E [X (X - 1)] & = \sum_{k = 2}^{n} n (n - 1)_{n - 2} C_{k - 2} p^{k} (1 - p)^{n - k} \\ = n (n - 1) p^{2} \sum_{m = 0}^{n - 2}_{n - 2} C_{m} p^{m} (1 - p)^{(n - 2) - m} . \end{aligned}

ここで $\sum_{m = 0}^{n - 2}_{n - 2} C_{m} p^{m} (1 - p)^{(n - 2) - m} = 1$ （全確率）より

E [X (X - 1)] = n (n - 1) p^{2} .

ゆえに

E [X^{2}] = E [X (X - 1)] + E [X] = n (n - 1) p^{2} + n p,

したがって

V [X] = (n (n - 1) p^{2} + n p) - (n p)^{2} = n p (1 - p) .

5. 積率母関数

積率母関数 (MGF)

M_{X} (t) = E [e^{t X}] = (1 - p + p e^{t})^{n} .

導出の手順はこちら

導出

独立性と $I_{i} \in {0, 1}$ から
\begin{align}
M_X(t)&=\mathbb{E}!\left[e^{t\sum I_i}\right]=\prod_{i=1}^{n\mathbb{E}[e}]
=\bigl((1-p)+p e^{t}\bigr)n.
\end

6. 特性関数

特性関数 (CF)

φ_{X} (ω) = E [e^{i ω X}] = (1 - p + p e^{i ω})^{n} .

導出の手順はこちら

導出

MGF と同様に

φ_{X} (ω) = \prod_{i = 1}^{n} E [e^{i ω I_{i}}] = ((1 - p) + p e^{i ω})^{n} .

二項分布の性質

二項分布の性質

1. 確率質量関数

2. 累積分布関数

3. 期待値

4. 分散

5. 積率母関数

6. 特性関数

参考文献

増訂版日本統計学会公式認定統計検定１級対応統計学

新装改訂版　現代数理統計学