t分布の性質

t分布は 分散が未知の場合の仮説検定でよく使用される分布 です.

t分布もしくは スチューデントのt分布 と言われます.

定義にある標準正規分布とカイ二乗分布との関係は必ず覚えた方がいいでしょう. (統計検定には頻出！)

定義

$Y\sim \mathcal{N}(0,1)$, $X\sim {\chi }^2(n)$, かつ $Y\perp X$ (独立)のとき,

$$T=\frac{Y}{\sqrt{X/n}}\sim t(n)$$

は自由度 $n$ の $t$ 分布に従う.
ただし, $Y$ は標準正規分布, $X$ は自由度 $n$ のカイ二乗分布を表す.

1. 確率密度関数

確率密度関数 (PDF)

自由度 $n$ の $t$ 分布 $T\sim t(n)$ の確率密度関数は

$$f(t)=\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}{(1+\frac{t^2}{n})}^{-\frac{n+1}{2}}$$

また $n=1$　のとき,

$$\begin{array}{rl}f(t)& =\frac{\mathrm{\Gamma }\left(1\right)}{\sqrt{\pi }\mathrm{\Gamma }\left(\frac{1}{2}\right)}{(1+t^2)}^{-1}\\ & =\frac{1}{\pi (1+t^2)}\end{array}$$

これを特別に(標準) コーシー分布 という.

確率密度関数のグラフ

解説

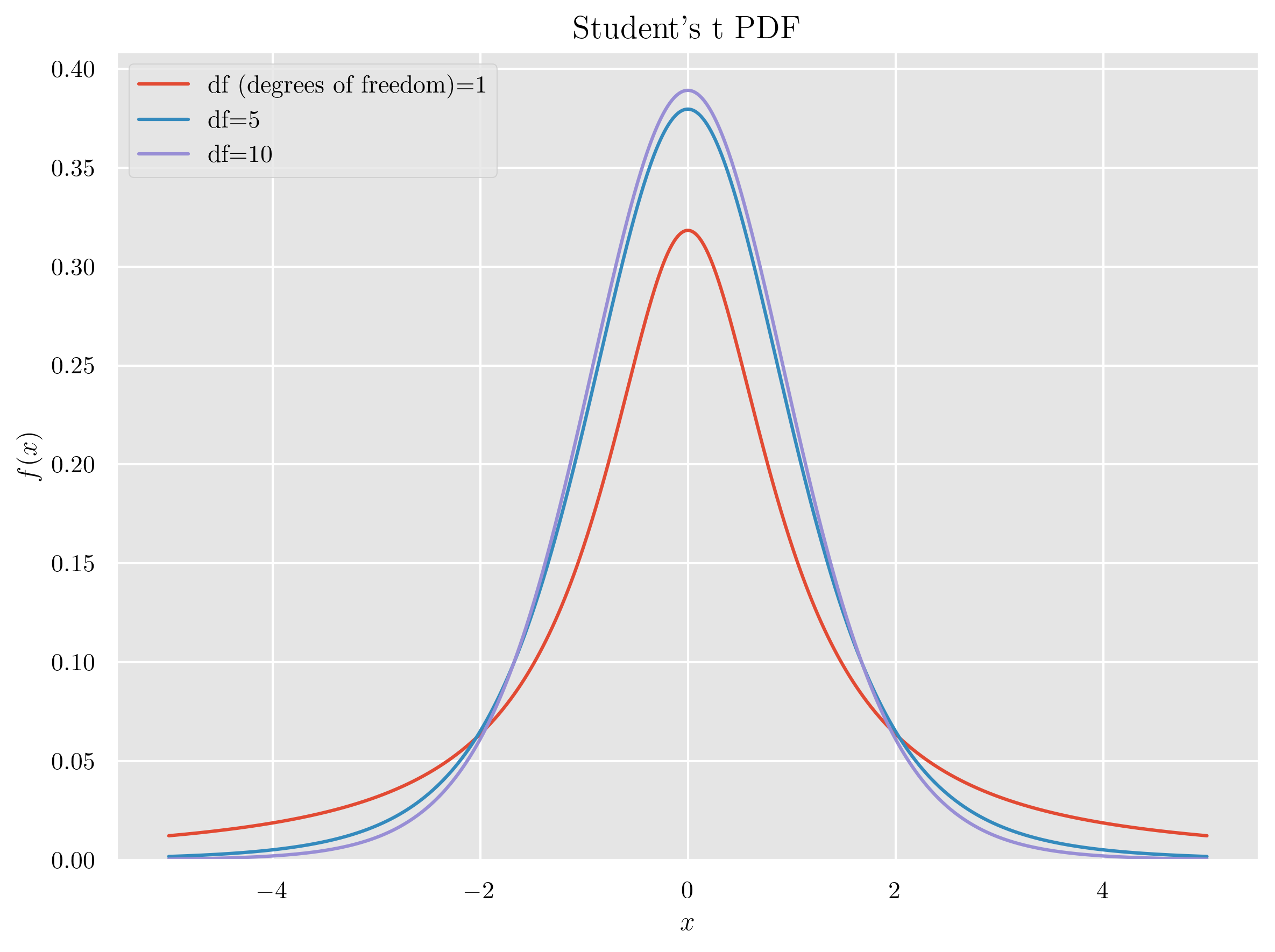
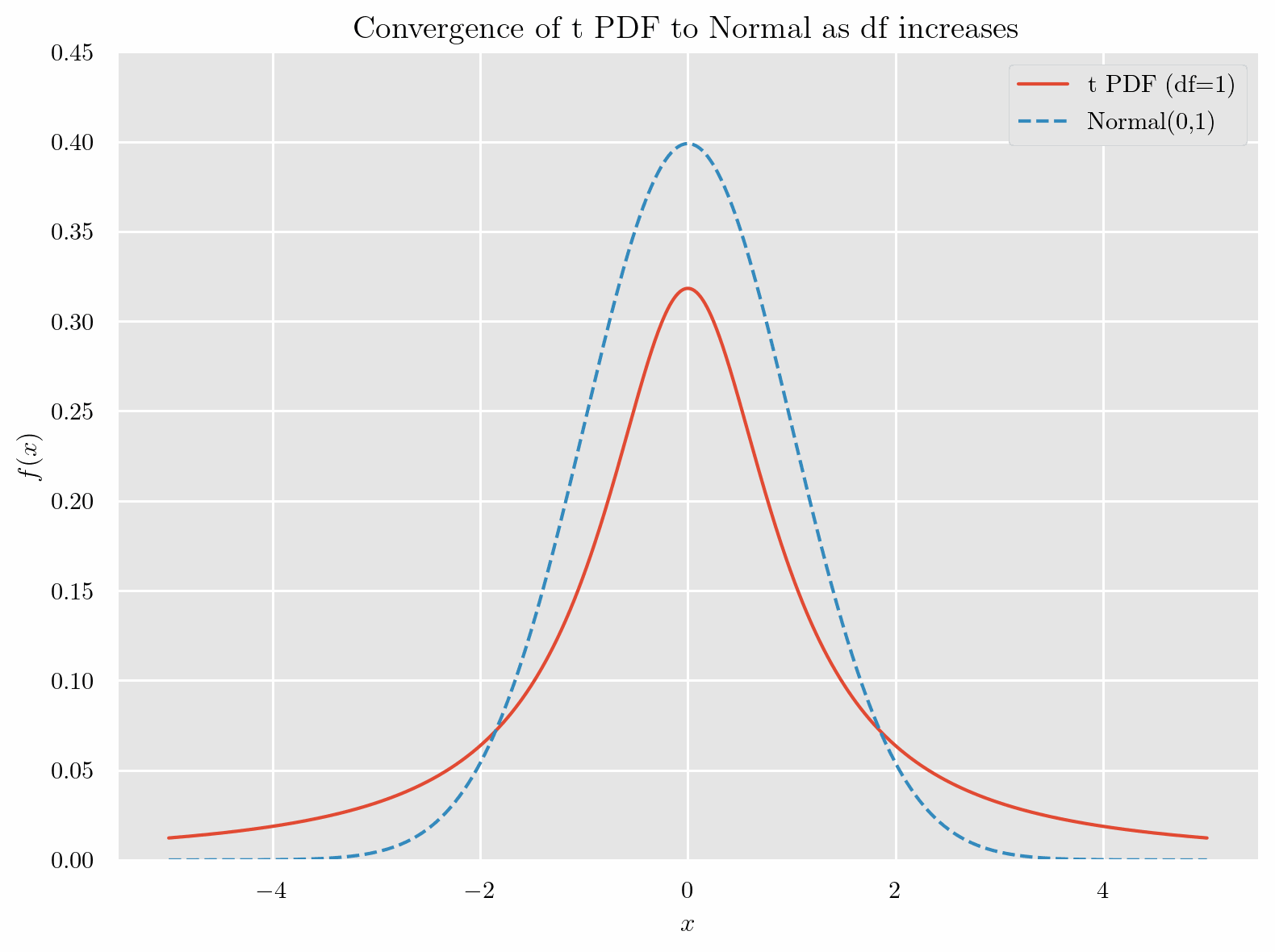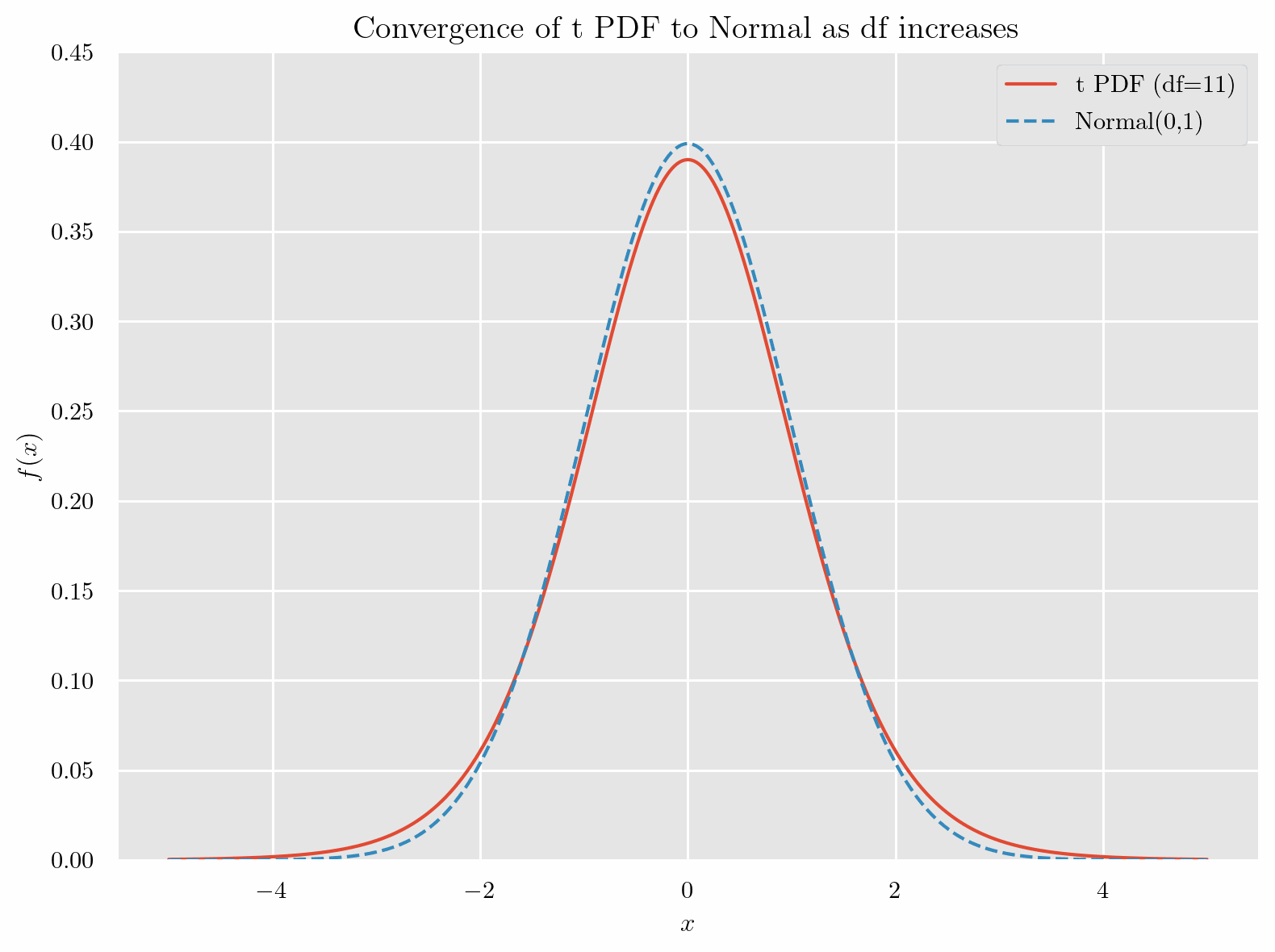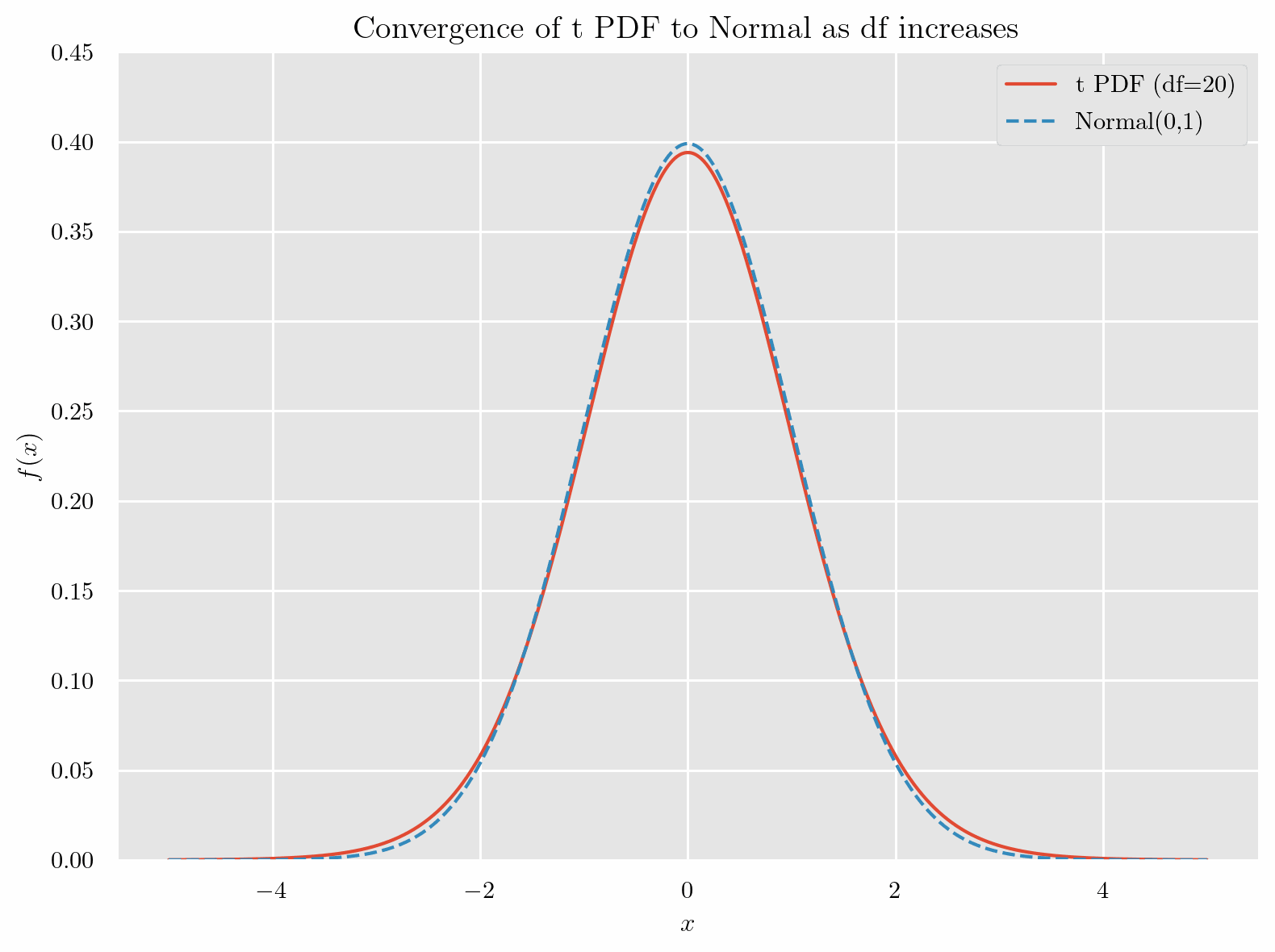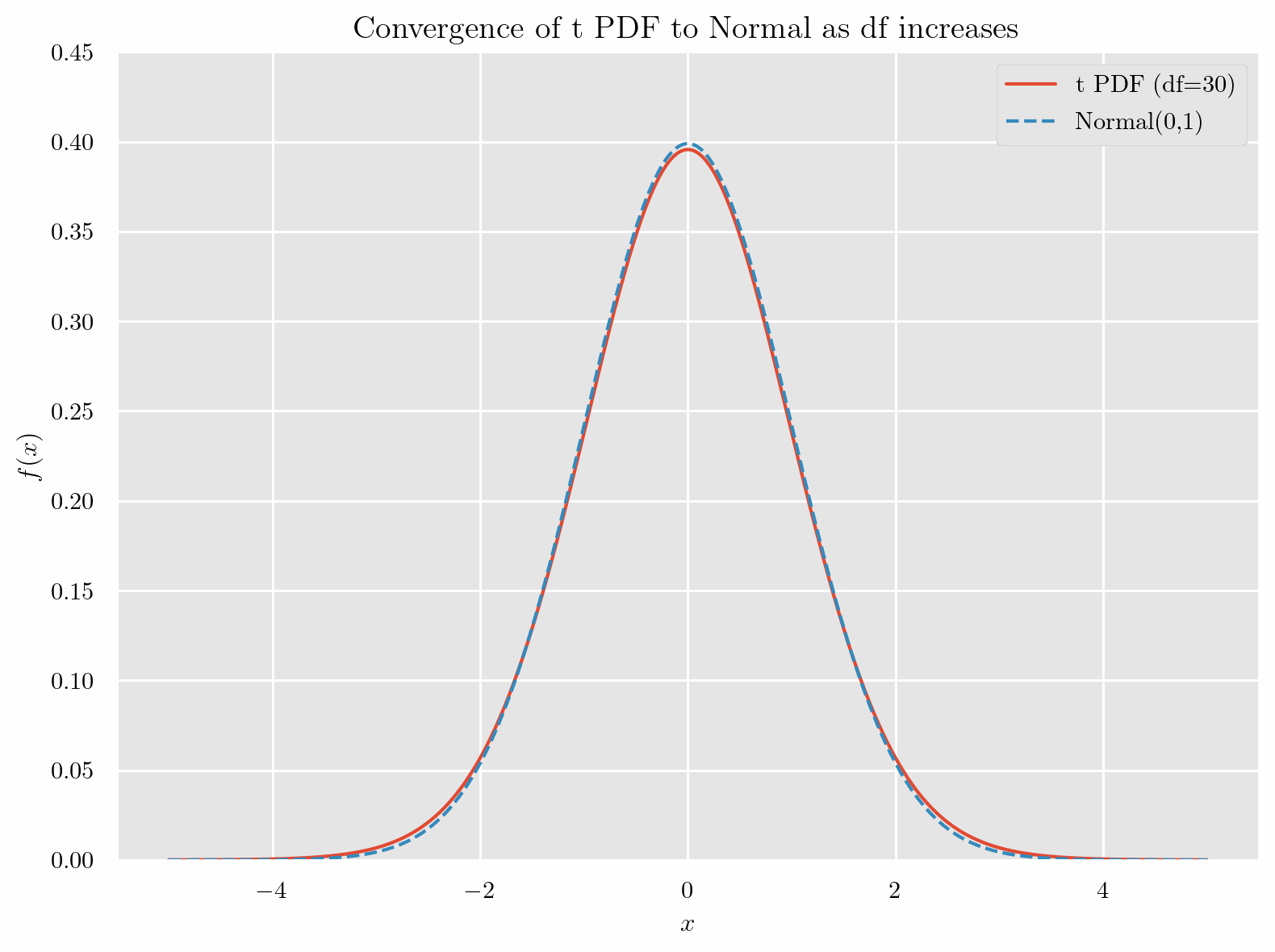
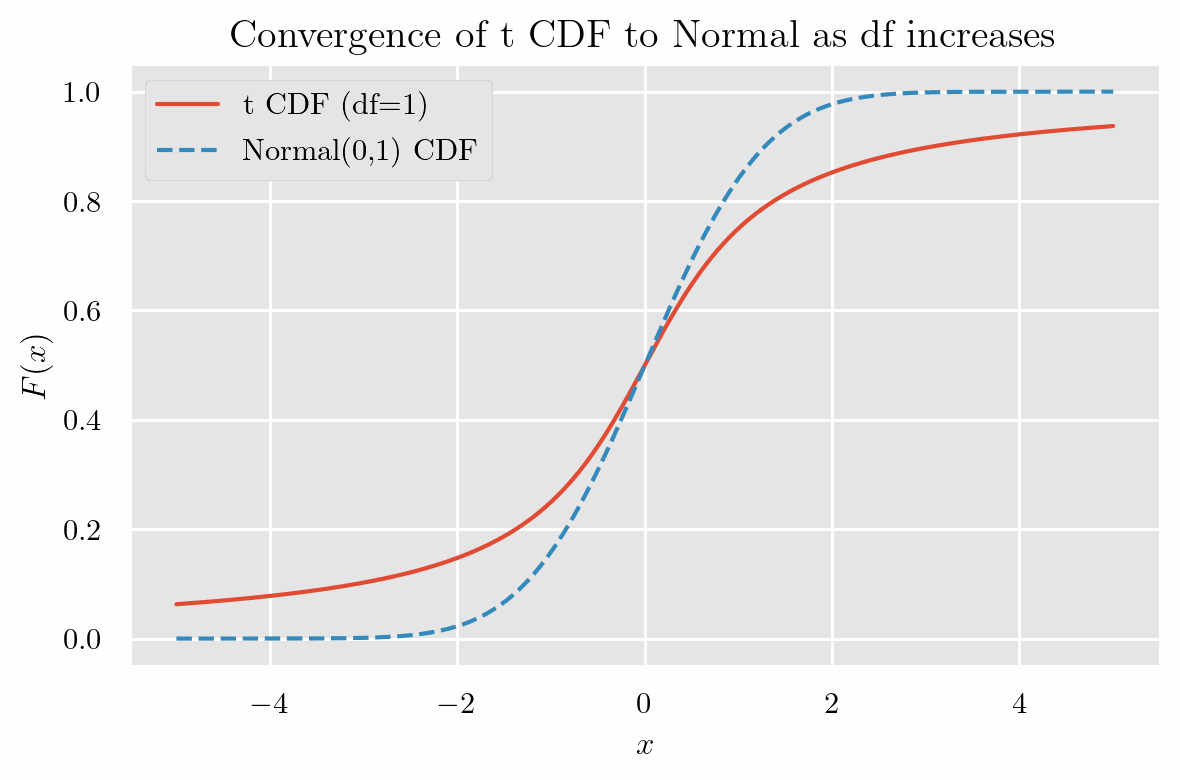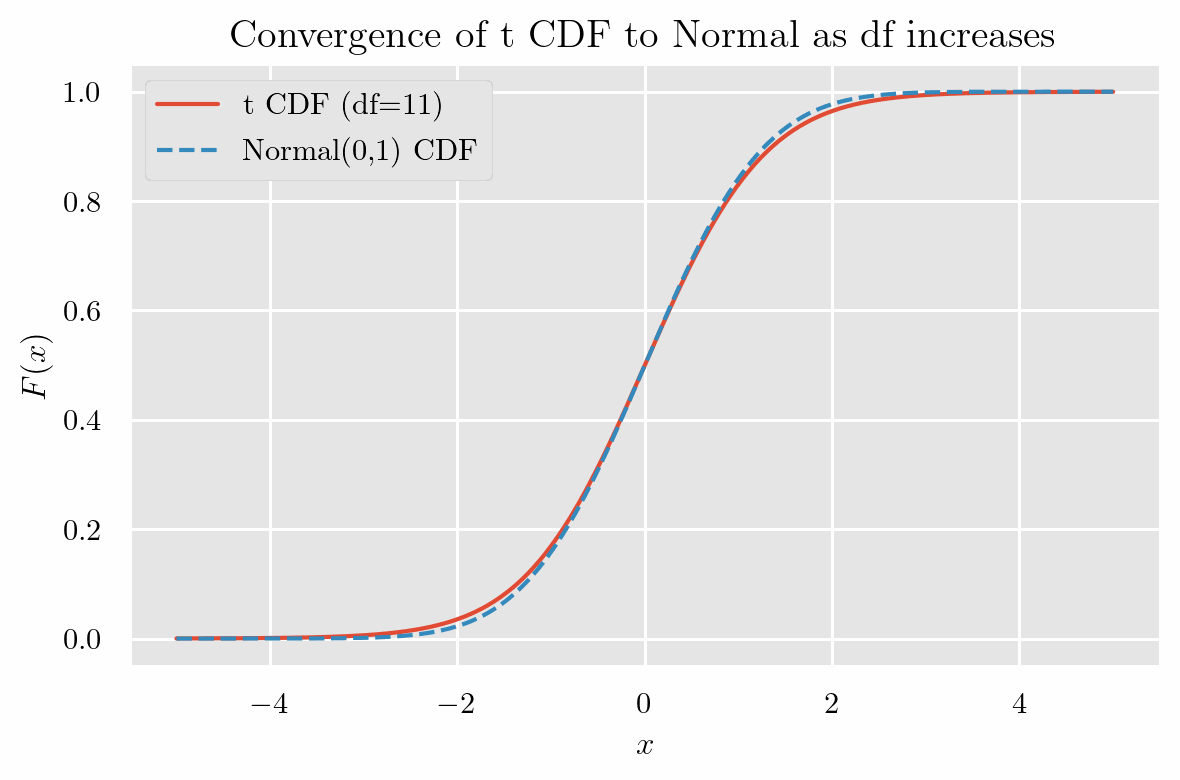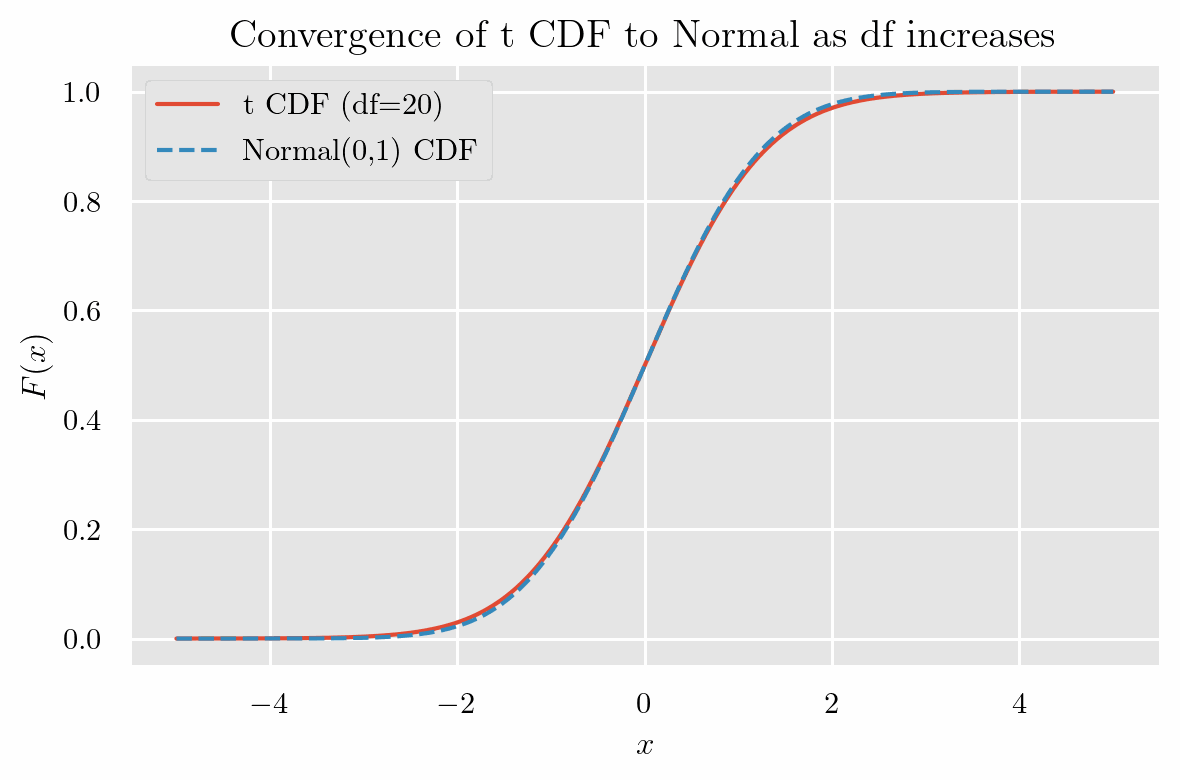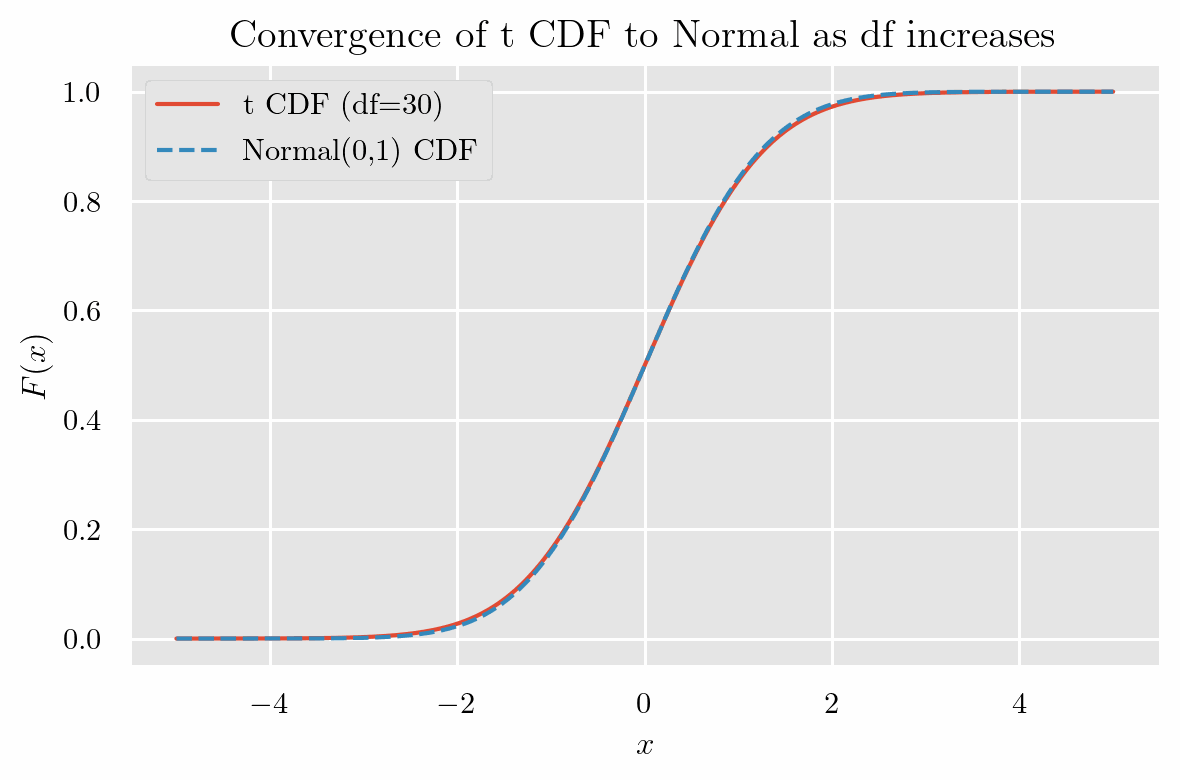
標準正規分布と非常によく似た形をしていて、自由度(degrees of freedom)が増えるにつれて

標準正規分布と一致 するようすが確認できます.

特徴として、自由度が小さい場合, 標準正規分布より 山が低く、裾が厚い です.

t分布の確率密度関数の導出は

• 変数変換
• ヤコビアンの計算
• ガンマ関数の定義

などなど為になる計算が豊富です.ぜひ理解してできるようにしてください.

おすすめ

導出には標準正規分布とカイ二乗分布を使用します.二つの分布についてはこちらをご覧ください.

標準正規分布の性質

---

期待値・分散・導出

カイ二乗分布の性質

---

期待値・分散・導出

導出の手順はこちら

導出

$Y\sim \mathcal{N}(0,1)$, $X\sim {\chi }^2(n)$, かつ $Y\perp X$ (独立)のとき,
それぞれの周辺確率密度関数を $f_X(x),f_Y(y)$とする.

$$\begin{array}{rl}{f}_X(x)& =\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{x}^{\frac{n}{2}-1}{e}^{-\frac{x}{2}}\\ f_Y(y)& =\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{y}^2}\end{array}$$

$T={\displaystyle \frac{Y}{\sqrt{X/n}}},U=X$ で変数変換.

• 逆変換
  $x=u,y=\sqrt{{\displaystyle \frac{u}{n}}}t$

• ヤコビアン $|J|$

$$\begin{array}{rl}J& =\left(\begin{array}{cc}\frac{\partial x}{\partial t}& \frac{\partial x}{\partial u}\\ \frac{\partial y}{\partial t}& \frac{\partial y}{\partial u}\end{array}\phantom{\begin{array}{cc}0& 1\\ \sqrt{{\displaystyle \frac{u}{n}}}& {\displaystyle \frac{t}{2\sqrt{un}}}\end{array}}\right)\\ & =\left(\begin{array}{cc}0& 1\\ \sqrt{{\displaystyle \frac{u}{n}}}& {\displaystyle \frac{t}{2\sqrt{un}}}\end{array}\right)\end{array}$$$$\begin{array}{rl}|J|& =|0\cdot \frac{t}{2\sqrt{un}}-1\cdot \sqrt{\frac{u}{n}}|\\ & =\sqrt{\frac{u}{n}}\end{array}$$

したがって $U,T$ の同時分布 $f(u,t)$ は,

$$\begin{array}{rl}f(u,t)& =f(x,y)|J|\\ & =f_X(x)f_Y(y)\sqrt{\frac{u}{n}}\\ & =f_X(u)f_Y\left(\sqrt{\frac{u}{n}}t\right)\sqrt{\frac{u}{n}}\\ & =\frac{1}{2^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{u}^{\frac{n}{2}-1}{e}^{-\frac{u}{2}}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{u}{2n}{t}^2}\sqrt{\frac{u}{n}}\\ & =\frac{1}{\sqrt{2n\pi }{2}^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{u}^{\frac{n-1}{2}}{e}^{-\frac{1}{2}u(1+\frac{t^2}{n})}\end{array}$$

ここで周辺化して $T$ の確率密度関数 $f_T(t)$ を求めると,

$$\begin{array}{rl}{f}_T(t)& ={\int }_0^{\mathrm{\infty }}f(u,t)du\\ & =\frac{1}{\sqrt{2n\pi }{2}^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{u}^{\frac{n-1}{2}}{e}^{-\frac{1}{2}u(1+\frac{t^2}{n})}du\end{array}$$

ここで指数部分を文字で置いて見通しを良くしましょう.

• $a=\frac{n-1}{2},b=\frac{1}{2}(1+\frac{t^2}{n})$

$$\begin{array}{rl}{f}_T(t)& =\frac{1}{\sqrt{2n\pi }{2}^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}{\int }_0^{\mathrm{\infty }}{u}^a{e}^{-bu}du\end{array}$$

この式の積分部分を $I$ とすると

$$\begin{array}{rl}I& ={\int }_0^{\mathrm{\infty }}{u}^a{e}^{-bu}du\end{array}$$

$z=bu$ で置換積分すると

$$\begin{array}{rl}I& ={\int }_0^{\mathrm{\infty }}{\left(\frac{z}{b}\right)}^a{e}^{-z}\frac{1}{b}dz\\ & =\frac{1}{b^{a+1}}{\int }_0^{\mathrm{\infty }}{z}^a{e}^{-z}dz\\ & =\frac{1}{b^{a+1}}{\int }_0^{\mathrm{\infty }}{z}^{(a+1)-1}{e}^{-z}dz\end{array}$$

ガンマ関数 の定義より,

$$\begin{array}{rl}I& =\frac{1}{b^{a+1}}\mathrm{\Gamma }(a+1)\\ & =\frac{1}{b^{a+1}}\mathrm{\Gamma }\left(\frac{n+1}{2}\right)\end{array}$$

さて $f_T(t)$ は,

$$\begin{array}{rl}{f}_T(t)& =\frac{1}{\sqrt{2n\pi }{2}^{n/2}\mathrm{\Gamma }\left(\frac{n}{2}\right)}\frac{1}{b^{a+1}}\mathrm{\Gamma }\left(\frac{n+1}{2}\right)\\ & =\frac{1}{\sqrt{n\pi }{2}^{\frac{n+1}{2}}\mathrm{\Gamma }\left(\frac{n}{2}\right)}\frac{1}{b^{\frac{n+1}{2}}}\mathrm{\Gamma }\left(\frac{n+1}{2}\right)\\ & =\frac{1}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}\mathrm{\Gamma }\left(\frac{n+1}{2}\right)(2b{)}^{-\frac{n+1}{2}}\\ & =\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}{(1+\frac{t^2}{n})}^{-\frac{n+1}{2}}\end{array}$$

導出終了.

2. 累積分布関数

累積分布関数 (CDF)

自由度 $n$ の $t$ 分布 $T\sim t(n)$ の累積分布関数は
初等関数での閉じた形はなく，正則不完全ベータ関数 $I$ で表す
(統計検定の範囲外なので紹介のみ)

$$\begin{array}{rl}F(t)={\int }_{-\mathrm{\infty }}^{t}f(u)du& =1-\frac{1}{2}{I}_{x(t)}(\frac{n}{2},\frac{1}{2})\end{array}$$

ただし $x(t)=\frac{n}{t^2+n}$

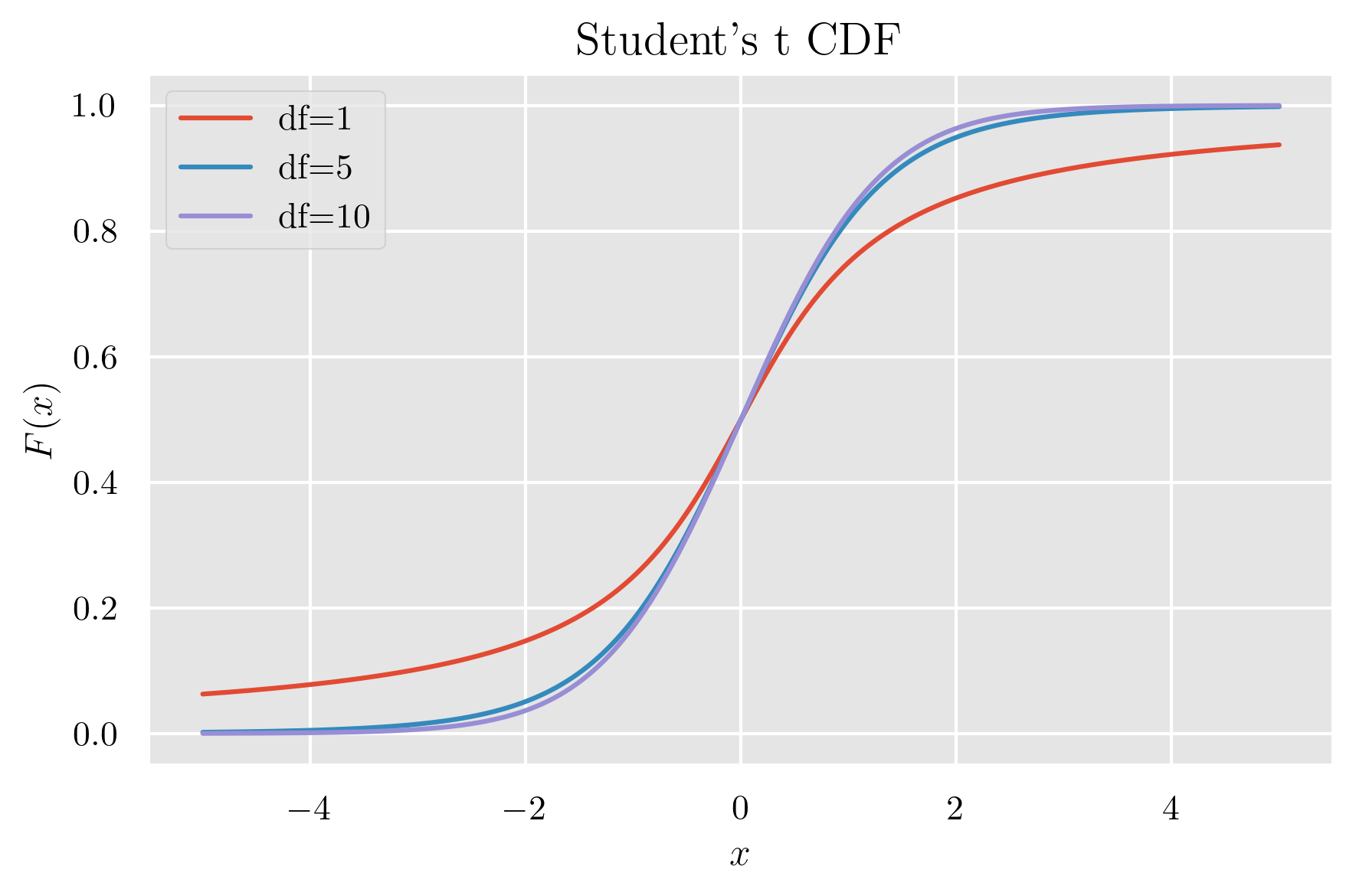
累積分布関数のグラフ

3. 期待値

期待値 (Mean)

$t$ 分布 $T\sim t(n)$ の期待値は

$$\mathbb{E}[T]=\{\begin{array}{ll}0,& n>1,\\ \text{未定義},& 0<n\le 1.\end{array}$$

（対称性により存在すれば 0, 存在条件は $n>1$）

興味深いのは $0<n\le 1$ つまり コーシー分布のときでも期待値が定義されません.

導出の手順はこちら

導出

PDF を

$$f(t)=C{(1+\frac{t^2}{n})}^{-\frac{n+1}{2}},C=\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}$$

とする.

対称性 $f(t)=f(-t)$ より，期待値が存在すれば $\mathbb{E}[T]=0$.

4. 分散

分散

$t$ 分布 $T\sim t(n)$ の分散は

$$\mathrm{V}[T]=\{\begin{array}{ll}{\displaystyle \frac{n}{n-2}},& n>2,\\ \text{未定義（発散）},& 1<n\le 2,\\ \text{未定義},& 0<n\le 1.\end{array}$$

（$n\le 1$ は平均が未定義. $1<n\le 2$ は平均は 0 だが二乗積分が発散）

導出の手順はこちら

導出

PDF を

$$f(t)=C{(1+\frac{t^2}{n})}^{-\frac{n+1}{2}},C=\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}$$

とする. 対称性より $n>1$ で $\mathbb{E}[X]=0$ なので $\mathrm{V}(X)=\mathbb{E}[X^2]$ を計算する.

$$\mathbb{E}[T^2]=2C{\int }_0^{\mathrm{\infty }}{t}^2{(1+\frac{t^2}{n})}^{-\frac{n+1}{2}}dt.$$

$u=t^2/n$で置換すると,

• 逆変換 $t=\sqrt{nu}$
• 微分 $dt=\frac{\sqrt{n}}{2}{u}^{-1/2}du$
• 範囲 $t:0\to \mathrm{\infty },u:0\to \mathrm{\infty }$

$$\begin{array}{rl}\mathbb{E}[T^2]& =C{n}^{3/2}{\int }_0^{\mathrm{\infty }}{u}^{1/2}(1+u{)}^{-\frac{n+1}{2}}du\end{array}$$

ここで $z=\frac{u}{1+u}$ とおくと

• 逆変換 $u=\frac{z}{1-z}$
• 微分 $du=\frac{1}{(1-z{)}^2}dz$
• 範囲 $u:0\to \mathrm{\infty },z:0\to 1$

$$\begin{array}{rl}\mathbb{E}[T^2]& =C{n}^{3/2}{\int }_0^1{\left(\frac{z}{1-z}\right)}^{\frac{1}{2}}{\left(\frac{1}{1-z}\right)}^{-\frac{n+1}{2}}\frac{1}{(1-z{)}^2}dz\\ & =C{n}^{3/2}{\int }_0^1{z}^{\frac{1}{2}}(1-z{)}^{\frac{n-4}{2}}dz\\ & =C{n}^{3/2}{\int }_0^1{z}^{\frac{3}{2}-1}(1-z{)}^{\frac{n-2}{2}-1}dz\\ & =C{n}^{3/2}\mathrm{B}(\frac{3}{2},\frac{n-2}{2})\end{array}$$

ただし $\mathrm{B}$ はベータ関数.

ここからベータ関数とガンマ関数の性質を使用するときれいに約分できます.

• $\mathrm{B}(x,y)=\frac{\mathrm{\Gamma }(x)\mathrm{\Gamma }(y)}{\mathrm{\Gamma }(x+y)}$
• $\mathrm{\Gamma }(x+1)=x\mathrm{\Gamma }(x)$

さて $C$ も代入して丁寧に整理していきましょう.

$$\begin{array}{rl}\mathbb{E}[T^2]& =\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\sqrt{n\pi }\mathrm{\Gamma }\left(\frac{n}{2}\right)}n\sqrt{n}\mathrm{B}(\frac{3}{2},\frac{n-2}{2})\\ & =\frac{n}{\sqrt{\pi }}\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}\mathrm{B}(\frac{3}{2},\frac{n-2}{2})\\ & =\frac{n}{\sqrt{\pi }}\frac{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}\frac{\mathrm{\Gamma }\left(\frac{3}{2}\right)\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\mathrm{\Gamma }\left(\frac{n+1}{2}\right)}\\ & =\frac{n}{\sqrt{\pi }}\cdot \frac{\mathrm{\Gamma }\left(\frac{3}{2}\right)\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}\\ & =\frac{n}{\sqrt{\pi }}\cdot \frac{\frac{\sqrt{\pi }}{2}\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}\\ & =\frac{n}{2}\cdot \frac{\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\mathrm{\Gamma }\left(\frac{n}{2}\right)}\\ & =\frac{n}{2}\cdot \frac{\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\mathrm{\Gamma }(\frac{n}{2}-1+1)}\\ & =\frac{n}{2}\cdot \frac{\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}{\frac{n-2}{2}\mathrm{\Gamma }\left(\frac{n-2}{2}\right)}\\ & =\frac{n}{2}\cdot \frac{1}{\frac{n-2}{2}}\\ & =\frac{n}{n-2}.\end{array}$$

したがって,

$$\mathbb{E}[T^2]=\frac{n}{n-2}(n>2).$$

ゆえに $n>2$ で $\mathrm{V}[T]={\displaystyle \frac{n}{n-2}}$. 一方 $1<n\le 2$ はベータ積分が発散し分散は未定義. $n\le 1$ は平均も未定義.

参考文献

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る