ガンマ二乗分布の性質

解説

ガンマ分布は指数分布の和で定義されます.

独立同分布な待ち時間 $T_i\sim \mathrm{Exp}(\lambda )$（率 $\lambda >0$）とする. 尺度は $\theta =1/\lambda$.

このとき，和

$$\begin{array}{rl}{T}_k& =\sum _{i=1}^k{T}_i\sim \mathrm{Gamma}(k,\theta =1/\lambda )\end{array}$$

となる. ここで $k$ は形状パラメータ，$\theta$ は尺度パラメータ.

例えば
「外来患者の到着が一定率のポアソン過程で $\lambda =1/\theta$ とする. このとき $k$ 人目までの累積待ち時間 $T_k$ は $\mathrm{Gamma}(k,\theta )$ に従う.」

$\lambda$ を使う流儀と　$\theta =\frac{1}{\lambda }$ を使う流儀があります.混乱するので気を付けましょう. 個人的には $\theta$ 派です.(統計検定では $\lambda$ が多いような...)

1. 確率密度関数

定義

形状 $k>0$, 尺度 $\theta >0$, $x>0$ に対して

$$\begin{array}{rl}f(x)& =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{x}^{k-1}{e}^{-x/\theta }\end{array}$$

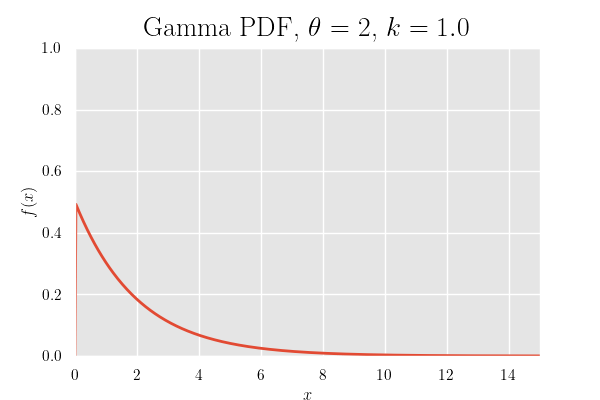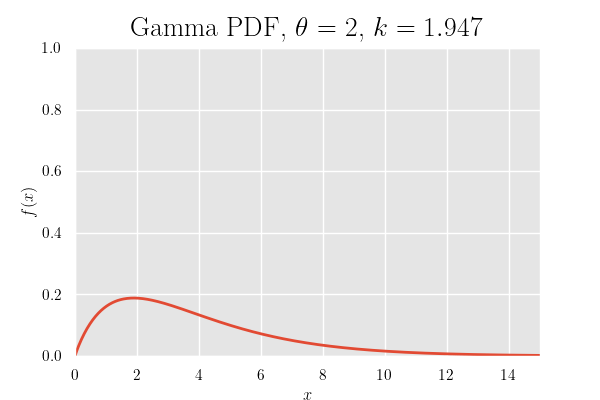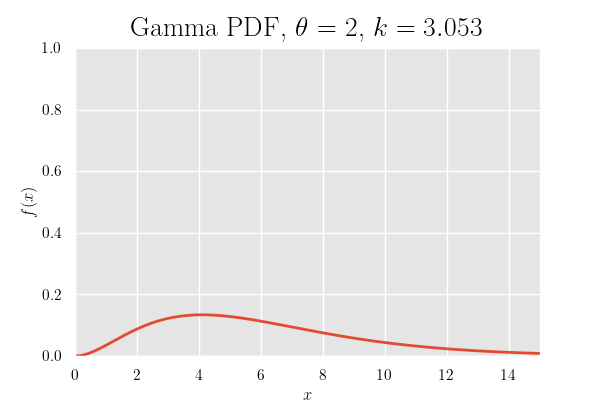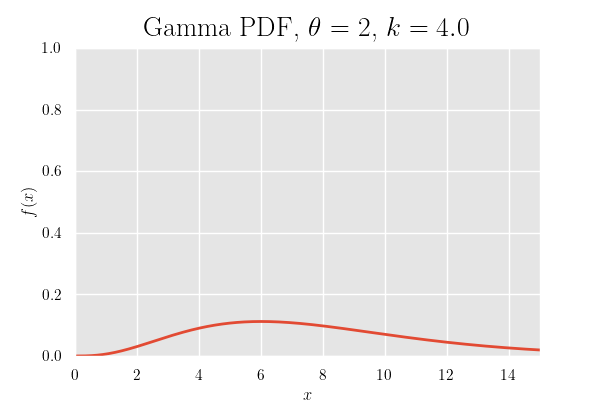
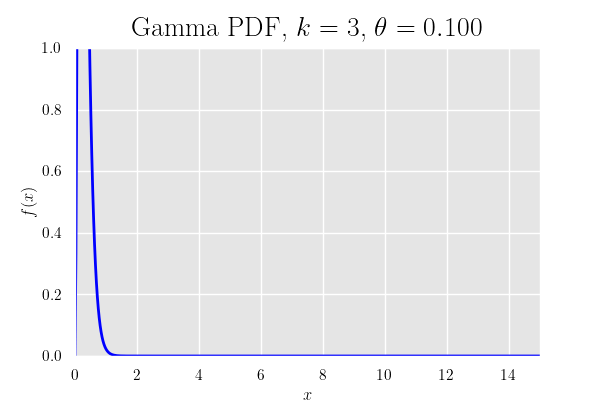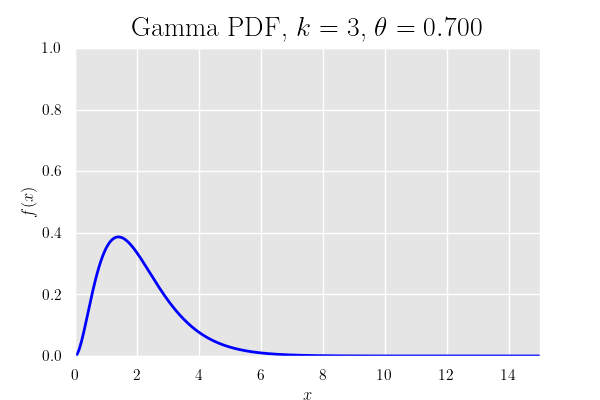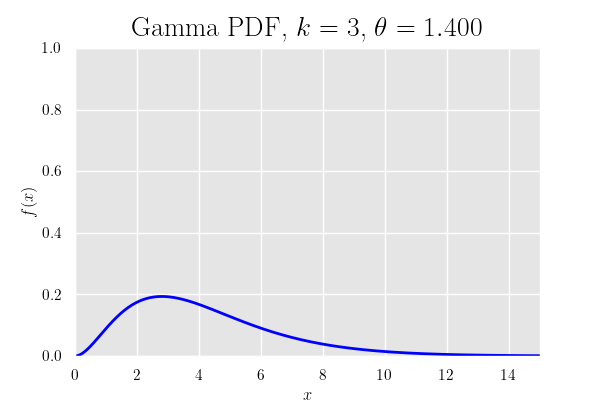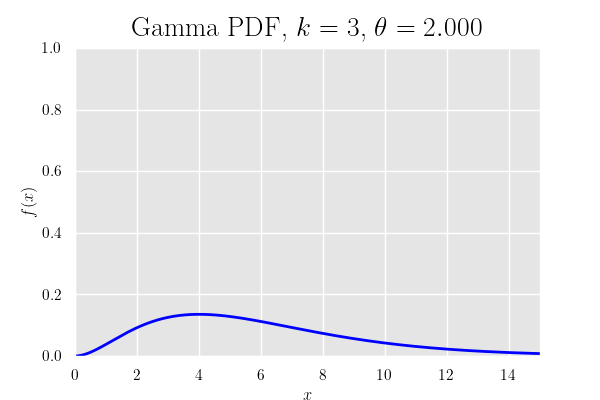
確率密度関数のグラフ

2. 累積分布関数

定義

$x>0$ に対して

$$\begin{array}{rl}F(x)& =Pr(X\le x)=\frac{\gamma (k,x/\theta )}{\mathrm{\Gamma }(k)}\end{array}$$

ここで $\gamma (k,z)={\int }_0^z{t}^{k-1}{e}^{-t}dt$ は第一種不完全ガンマ関数.

3. 期待値

期待値

$$\mathbb{E}[X]=k\theta$$

導出の手順はこちら

導出

ガンマ分布 $X\sim \mathrm{Gamma}(k,\theta )$ の密度は

$$f(x)=\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{x}^{k-1}{e}^{-x/\theta }(x>0)$$

より，

$$\begin{array}{rl}\mathbb{E}[X]& ={\int }_0^{\mathrm{\infty }}xf(x)dx=\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{x}^k{e}^{-x/\theta }dx\end{array}$$

と書ける．$u=x/\theta$ とおくと $x=\theta u,dx=\theta du$ で

$$\begin{array}{rl}\mathbb{E}[X]& =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}(\theta u{)}^k{e}^{-u}\theta du\\ & =\frac{{\theta }^{k+1}}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{u}^k{e}^{-u}du\\ & =\theta \cdot \frac{\mathrm{\Gamma }(k+1)}{\mathrm{\Gamma }(k)}\\ & =\theta \cdot k\\ & =k\theta \end{array}$$

4. 分散

分散

$$\mathrm{V}[X]=k{\theta }^2$$

導出の手順はこちら

導出

ガンマ分布 $X\sim \mathrm{Gamma}(k,\theta )$ に対して

$$\mathrm{V}[X]=\mathbb{E}[X^2]-\{\mathbb{E}[X]{\}}^2$$

より，まず $\mathbb{E}[X^2]$ を計算する.

$$\begin{array}{rl}\mathbb{E}[X^2]& ={\int }_0^{\mathrm{\infty }}{x}^{2}f(x)dx\\ & =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{x}^{k+1}{e}^{-x/\theta }dx\end{array}$$

$u=x/\theta$ とおく. すると $x=\theta u,dx=\theta du$.

$$\begin{array}{rl}\mathbb{E}[X^2]& =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}(\theta u{)}^{k+1}{e}^{-u}\theta du\\ & =\frac{{\theta }^{k+2}}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{u}^{k+1}{e}^{-u}du\\ & ={\theta }^2\frac{\mathrm{\Gamma }(k+2)}{\mathrm{\Gamma }(k)}\\ & ={\theta }^2\frac{k(k+1)\mathrm{\Gamma }(k)}{\mathrm{\Gamma }(k)}\\ & ={\theta }^{2}k(k+1).\end{array}$$

一方で $\mathbb{E}[X]=k\theta$ なので

$$\begin{array}{rl}\mathrm{V}[X]& ={\theta }^{2}k(k+1)-(k\theta {)}^2\\ & ={\theta }^2[k(k+1)-k^2]\\ & =k{\theta }^2.\end{array}$$

5. 積率母関数

積率母関数

$$M_X(t)=\mathbb{E}[e^{tX}]=(1-\theta t{)}^{-k}(t<1/\theta )$$

導出の手順はこちら

導出

ガンマ分布 $X\sim \mathrm{Gamma}(k,\theta )$ の密度

$$f(x)=\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{x}^{k-1}{e}^{-x/\theta }(x>0)$$

より

$$\begin{array}{rl}{M}_X(t)& ={\int }_0^{\mathrm{\infty }}{e}^{tx}f(x)dx\\ & =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{x}^{k-1}\exp (-(\frac{1}{\theta }-t)x)dx,\end{array}$$

ここで $t<1/\theta$ を仮定する.

$u=(\frac{1}{\theta }-t)x$ とおく.
すると $x={\displaystyle \frac{u}{\frac{1}{\theta }-t}}$, $dx={\displaystyle \frac{du}{\frac{1}{\theta }-t}}$.

$$\begin{array}{rl}{M}_X(t)& =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\int }_0^{\mathrm{\infty }}{\left(\frac{u}{\frac{1}{\theta }-t}\right)}^{k-1}{e}^{-u}\frac{du}{\frac{1}{\theta }-t}\\ & =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\left(\frac{1}{\frac{1}{\theta }-t}\right)}^k{\int }_0^{\mathrm{\infty }}{u}^{k-1}{e}^{-u}du\\ & =\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{\left(\frac{1}{\frac{1}{\theta }-t}\right)}^k\mathrm{\Gamma }(k)\\ & ={\left(\frac{1}{1-\theta t}\right)}^k\\ & =(1-\theta t{)}^{-k}.\end{array}$$

6. 特性関数

特性関数

$${\phi }_X(s)=\mathbb{E}[e^{isX}]=(1-i\theta s{)}^{-k}(s\in \mathbb{R})$$

導出の手順はこちら

導出

積率母関数が $M_X(t)=(1-\theta t{)}^{-k}$（$t<1/\theta$）なので，

$${\phi }_X(s)=M_X(is)=(1-i\theta s{)}^{-k}.$$

7. 再生性

注意

ガンマ分布は尺度パラメータが共通の場合のみ再生性があります.

定義

再生性は積率母関数を使うと簡単に証明できます.
確率変数 $X,Y$ は独立に $X\sim \mathrm{Gamma}(k_1,\theta )$, $Y\sim \mathrm{Gamma}(k_2,\theta )$ とする（同一の尺度 $\theta$）.

$Z=X+Y$ とおく.積率母関数 $M_X(t),M_Y(t),M_Z(t)$ について，独立性より

$$\begin{array}{rl}{M}_Z(t)& =M_X(t)M_Y(t)\\ & =(1-\theta t{)}^{-k_1}(1-\theta t{)}^{-k_2}\\ & =(1-\theta t{)}^{-(k_1+k_2)}(t<1/\theta )\end{array}$$

これは $\mathrm{Gamma}(k_1+k_2,\theta )$ の積率母関数であり，積率母関数の一意性から，

$$\begin{array}{r}Z\sim \mathrm{Gamma}(k_1+k_2,\theta )\end{array}$$

同様に $m$ 個の独立な $\mathrm{Gamma}(k_i,\theta )$ の和も $\mathrm{Gamma}(\sum _{i=1}^m{k}_i,\theta )$ に従う.

参考文献

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る