解説
正規分布は 線形変換で閉じている分布 です.
のとき, 変数変換 により
が成り立ちます.
したがって正規分布の多くの性質は 標準正規分布の変数変換 によって導出可能です(計算が容易になる).
正規分布が線形変換で閉じている証明
標準正規分布 の確率密度関数は
変数変換 を考える.
逆変換は で,ヤコビアンは .
したがって の密度関数は
これは平均 , 分散 の正規分布 の確率密度関数に一致する.
はじめに 👉 標準正規分布の性質 を確認することをおすすめします.
確率密度関数 (PDF)
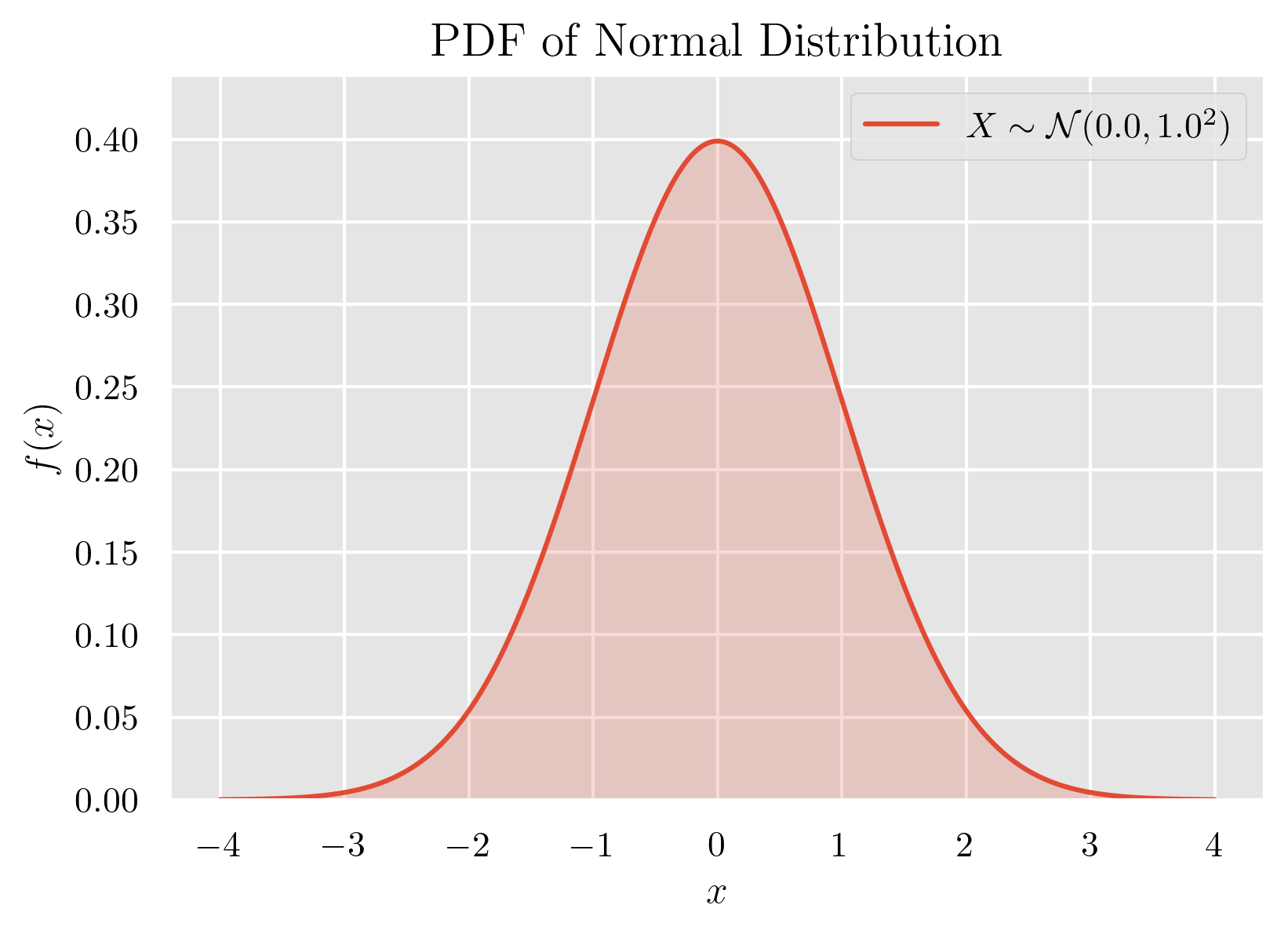
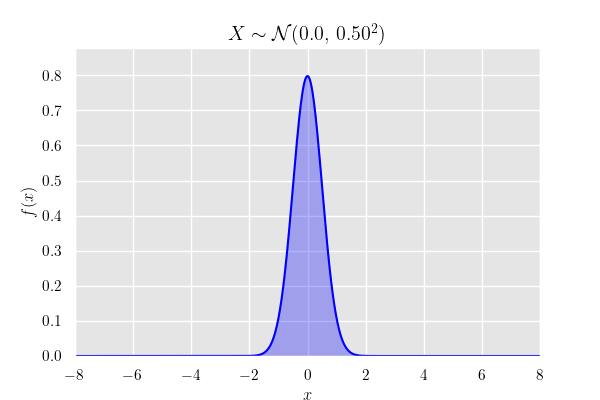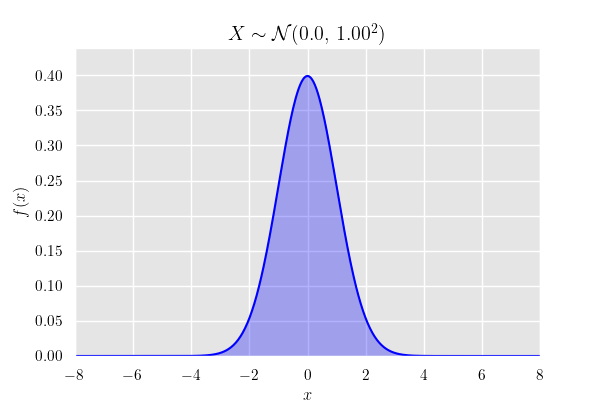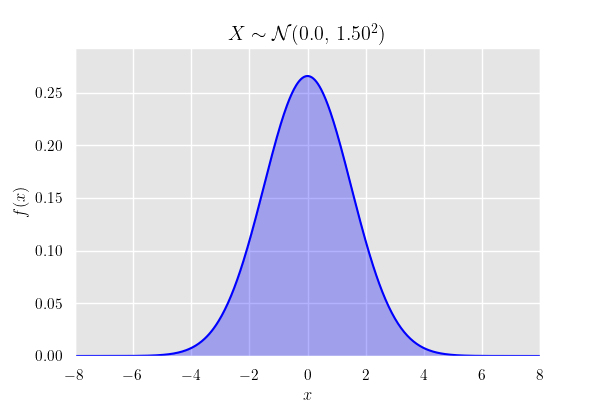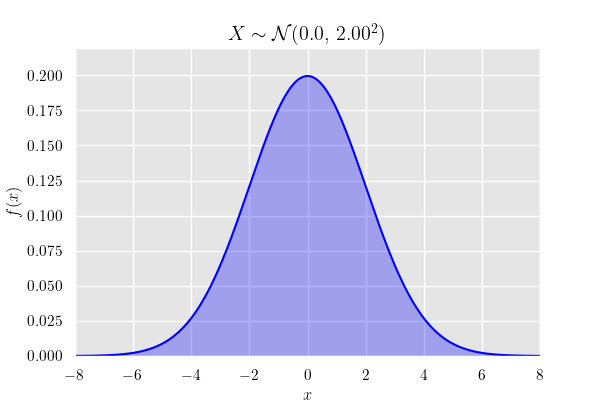
平均 , 分散 の正規分布 の確率密度関数は
確率密度関数のグラフ
累積分布関数 (CDF)
閉じた形は存在しませんが, 正則不完全ベータ関数を用いて,
のとき,,, とおくと
のとき .
等価に,符号で分けて
性質: 対称性より .
:::
誤差関数
積分を直接解くことはできないため,誤差関数 を導入する.
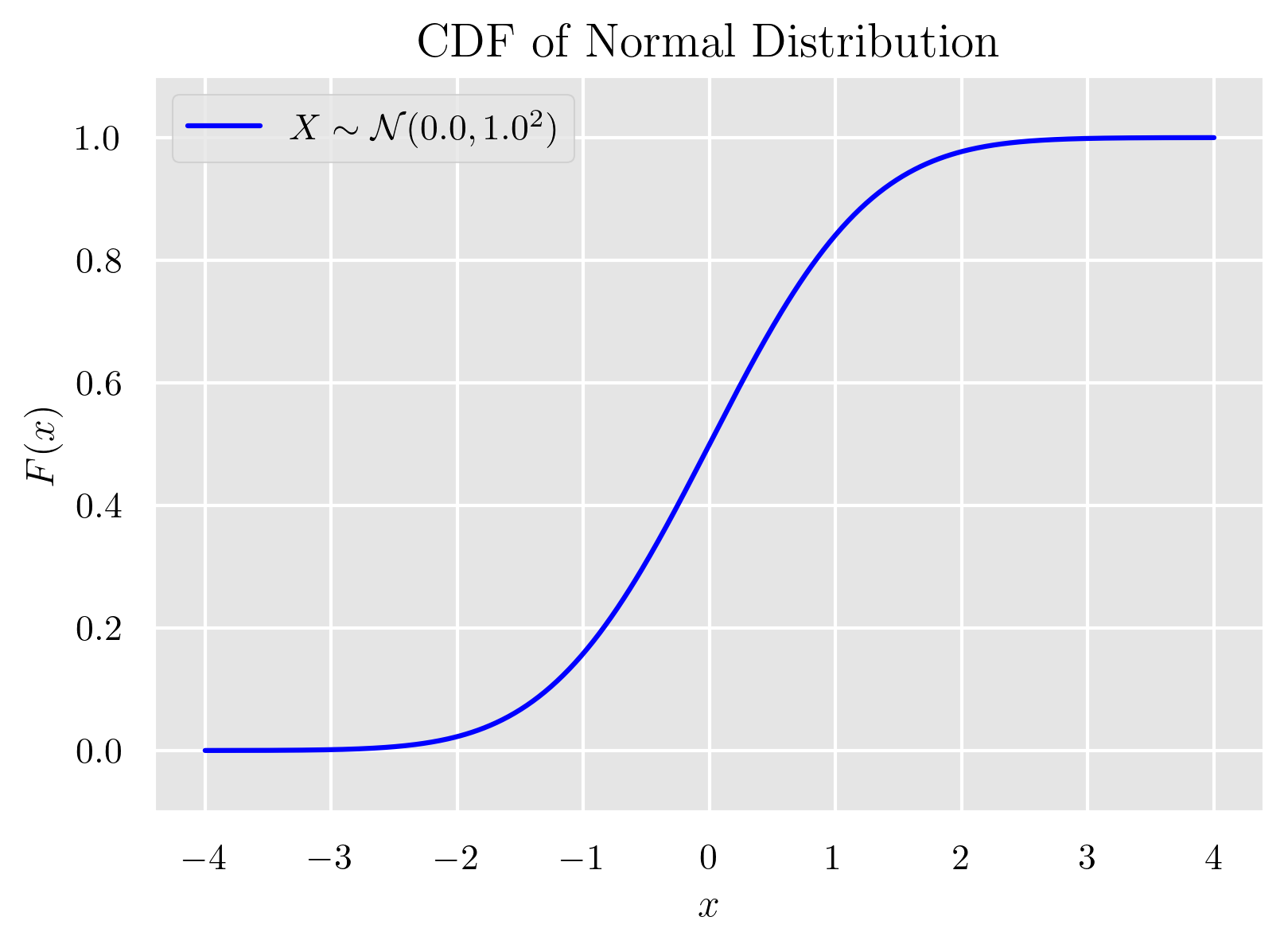
累積分布関数のグラフ
導出の手順はこちら
導出
平均 , 分散 の正規分布 に対して,
なので,
ここで変数変換を行う.
これを代入すると
積分を分けると
前者は標準正規分布の全確率で ,後者は奇関数の積分で .
したがって
導出の手順はこちら
導出
正規分布 に対して,分散は
である.
確率密度関数は
なので,
変数変換を行う.
代入すると,
ここで
である(標準正規分布の二次モーメント).
したがって
積率母関数 (MGF)
導出の手順はこちら
導出
標準正規分布 の積率母関数は
である.
いま を
と標準正規分布 を使って表す.
すると
指数を分けると
ここで は のMGFを とおいたものだから
したがって
これで導出が完了する.
特性関数 (CF)
導出の手順はこちら
導出
MGFと同様の積分を行い, を に置換して導出できる.

日本統計学会
統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

竹村 彰通
統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富