2013年 統計数理 問1

日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]

日本統計学会

過去問2012年・2013年

Amazonで見る

[1]は公式解説ではいきなり $X\sim \mathrm{Uniform}(0,\frac{1}{2})$ が既知となっていますが、既知とせず証明から解説しました.

[1] 期待値, 分散, 相関係数

問題設定の図

解答

上の図のように点を配置し, $\mathrm{\angle }AOB=u$ とする.

$u$ を表す確率変数を $U$ とすると $U$ は一様分布に従う. $U\sim \mathrm{Uniform}(0,2\pi )$

確率密度関数 $f_U(u)$ は

$$f_U(u)=\{\begin{array}{ll}{\displaystyle \frac{1}{2\pi }},& 0\le u\le 2\pi ,\\ 0,& \text{otherwise}.\end{array}$$

また確率変数 $X$ を $U$ を用いて表すと

$$X=\{\begin{array}{ll}{\displaystyle \frac{U}{2\pi }},& 0\le u<\pi ,\\ 1-{\displaystyle \frac{U}{2\pi }},& \pi \le u\le 2\pi ,\end{array}$$

それぞれで $X$ のとりうる値の範囲を考えると,

1. $0\le u<\pi \Rightarrow 0\le x<\frac{1}{2}$

2. $\pi \le u\le 2\pi \Rightarrow 0\le x\le \frac{1}{2}$

したがって1,2より $X$ の値の範囲は $0\le x\le \frac{1}{2}$

変数変換を考える.変数変換の公式は

$$f_X(x)=\sum _{u:g(u)=x}{f}_U(u)\left|\frac{du}{dx}\right|$$

で与えられる.

「$u:,g(u)=x$」について

用語

ここで「$u:,g(u)=x$」とは「方程式 $g(u)=x$ を満たすすべての $u$」を意味する.

本問では

• $0\le u<\pi$ のとき

  $$g(u)=\frac{u}{2\pi },g(u)=x\Rightarrow u=2\pi x.$$

• $\pi \le u\le 2\pi$ のとき

  $$g(u)=1-\frac{u}{2\pi },g(u)=x\Rightarrow u=2\pi (1-x).$$

したがって

$$u:g(u)=x\Rightarrow u=2\pi x\text{または}u=2\pi (1-x).$$

この 2 つの解に対応する密度の寄与を合計すれば、$f_X(x)$ が得られる.

それぞれの解に対してヤコビアン $\left|\frac{du}{dx}\right|$ を計算すると,

• $u=2\pi x$ のとき

$$\begin{array}{rl}\frac{du}{dx}& =2\pi \\ f_{X,1}(x)& =f_U(u)\left|\frac{du}{dx}\right|\\ & =\frac{1}{2\pi }\cdot 2\pi \\ & =1\end{array}$$

• $u=2\pi (1-x)$ のとき

$$\begin{array}{rl}\frac{du}{dx}& =-2\pi \\ \left|\frac{du}{dx}\right|& =2\pi \\ f_{X,2}(x)& =f_U(u)\left|\frac{du}{dx}\right|\\ & =\frac{1}{2\pi }\cdot 2\pi \\ & =1\end{array}$$

したがって

$$\begin{array}{rl}{f}_X(x)& =f_{X,1}(x)+f_{X,2}(x)\\ & =2,0\le x\le \frac{1}{2}\end{array}$$

また

$$\begin{array}{rl}{\int }_0^{1/2}{f}_X(x)dx& ={\int }_0^{1/2}2dx\\ & =1\end{array}$$

よって確率変数 $X$ は

$$X\sim \mathrm{Uniform}(0,\frac{1}{2})$$

に従う.

$X,Y$の期待値と分散

解答

$X$ の期待値は 一様分布 の公式から

$$\mathbb{E}[X]=\frac{a+b}{2}=\frac{0+\frac{1}{2}}{2}=\frac{1}{4}.$$

分散は同様に公式から

$$\mathrm{V}[X]=\frac{(b-a{)}^2}{12}=\frac{{(\frac{1}{2}-0)}^2}{12}=\frac{1}{48}.$$

また $Y=1-X$ より

$Y$ の期待値, 分散は

$$\mathbb{E}[Y]=\mathbb{E}[1-X]=1-\mathbb{E}[X]=1-\frac{1}{4}=\frac{3}{4}.$$$$\mathrm{V}[Y]=\mathrm{V}[1-X]=\mathrm{V}[X]=\frac{1}{48}.$$

$X,Y$の相関係数

解答

$X,Y$ の相関係数は分散と共分散を用いて,

$${\rho }_{X,Y}=\frac{\mathrm{Cov}[X,Y]}{\sqrt{\mathrm{V}[X]\mathrm{V}[Y]}}.$$

ここで

$$\begin{array}{rl}Y& =1-X\\ \Rightarrow \mathrm{Cov}[X,Y]& =\mathrm{Cov}[X,1-X].\end{array}$$

定数との共分散は 0 なので

ここで

$$\begin{array}{rl}Y& =1-X\\ \Rightarrow \mathrm{Cov}[X,Y]& =\mathrm{Cov}[X,1-X]\end{array}$$

定数との共分散は 0 なので

$$\begin{array}{rl}\mathrm{Cov}[X,Y]& =\mathrm{Cov}[X,1]-\mathrm{Cov}[X,X]\\ & =0-\mathrm{V}[X]\\ & =-\mathrm{V}[X]\end{array}$$

したがって

$$\begin{array}{rl}{\rho }_{X,Y}& =\frac{-\mathrm{V}[X]}{\sqrt{\mathrm{V}[X]\mathrm{V}[Y]}}\\ & =\frac{-\mathrm{V}[X]}{\mathrm{V}[X]}\\ & =-1\end{array}$$

[2] $\frac{X}{Y}$, 累積分布関数, 確率密度関数

解答

$$W=\frac{X}{Y}=\frac{X}{1-X}$$

$W$ は以下の変形により単調増加であることがわかる.

$$\begin{array}{r}W=\frac{1}{1-\frac{1}{X}}\end{array}$$

$0\le x\le \frac{1}{2}$より, $W$ の値域は, $0\le w\le 1$

また変数変換の公式より,

$$f_W(w)=f_X(x)\left|\frac{dx}{dw}\right|$$

逆変換は,

$$x=\frac{w}{1+w}$$

したがって,

$$\frac{dx}{dw}=\frac{1}{(1+w{)}^2}$$

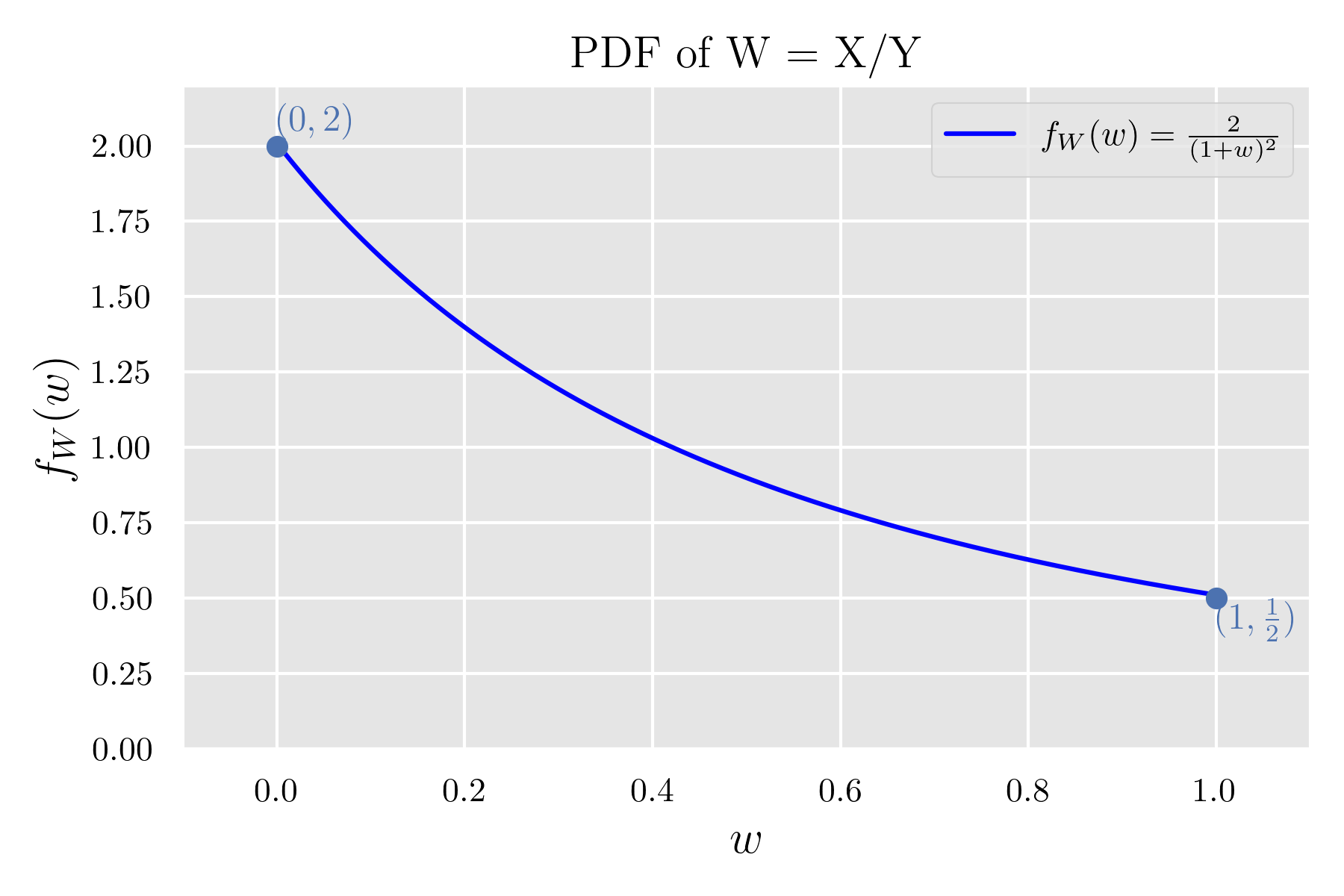
よって, $W$ の確率密度関数は

$$f_W(w)=\{\begin{array}{ll}{\displaystyle \frac{2}{(1+w{)}^2}},& 0\le w\le 1,\\ 0,& \text{otherwise}.\end{array}$$

確率密度関数の概形

解答

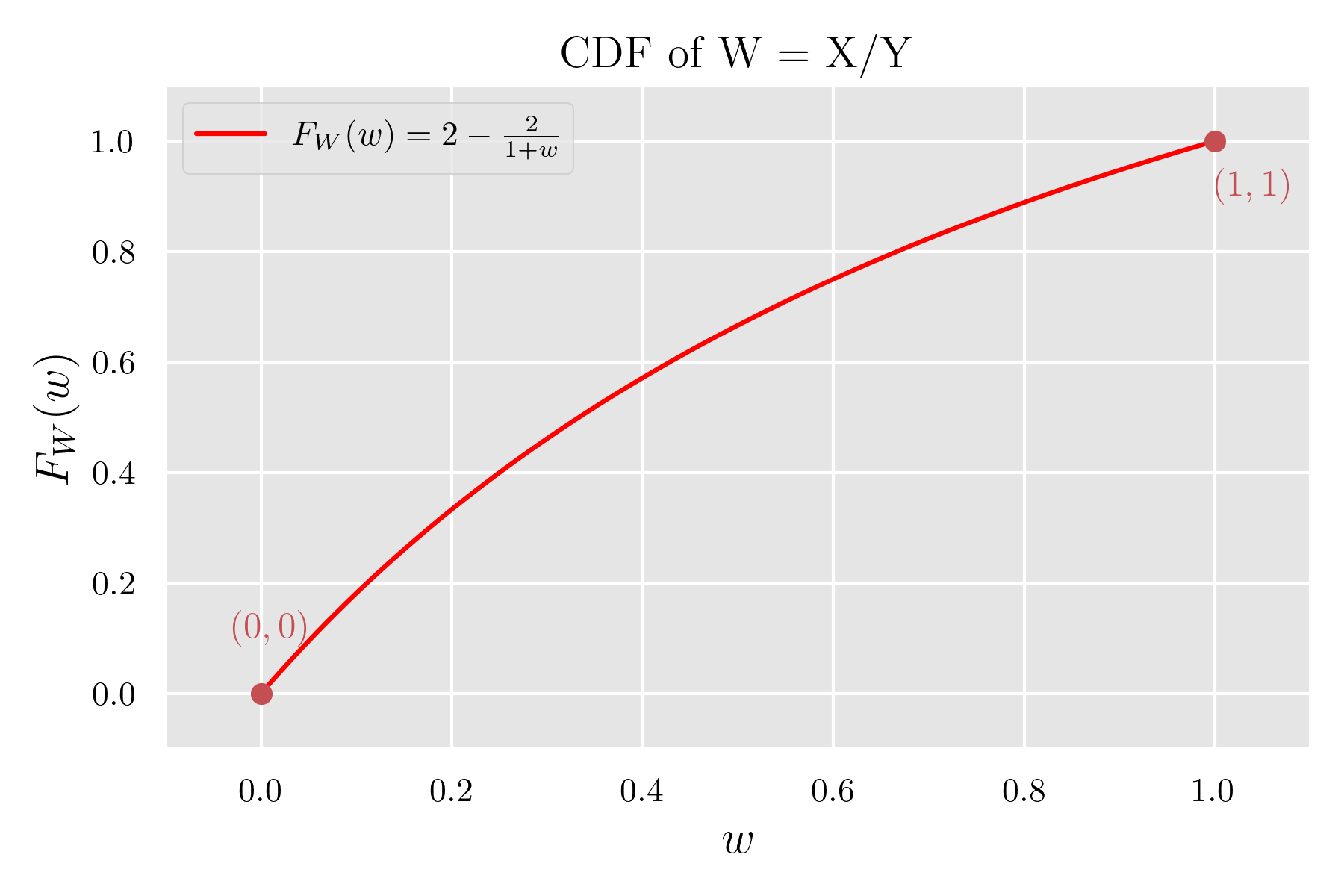
$W$ の累積分布関数は,

$$\begin{array}{rl}{F}_W(w)& =\mathbb{P}(W\le w)\\ & ={\int }_0^w{f}_W(t)dt\\ & ={\int }_0^w{\displaystyle \frac{2}{(1+t{)}^2}}dt\\ & =2-{\displaystyle \frac{2}{1+w}}\end{array}$$

したがって

$$F_W(w)=\{\begin{array}{ll}0,& w\le 0,\\ 2-{\displaystyle \frac{2}{1+w}},& 0<w<1,\\ 1,& w\ge 1.\end{array}$$

累積分布関数の概形

[3] $W$ の期待値と中央値

解答

期待値は,

$$\begin{array}{rl}\mathbb{E}[W]& ={\int }_0^{1}w{f}_W(w)dw\\ & ={\int }_0^1\frac{2w}{(1+w{)}^2}dw\\ & ={\int }_0^1\frac{2(1+w)-2}{(1+w{)}^2}dw\\ & ={\int }_0^1(\frac{2}{1+w}-\frac{2}{(1+w{)}^2})dw\\ & ={[2\ln (1+w)]}_0^1-{[-\frac{2}{1+w}]}_0^1\\ & =(2\ln 2-0)-(-1+2)\\ & =2\ln 2-1.\end{array}$$

---

中央値 $m$ は

$$F_W(m)=\frac{1}{2}$$

を満たす $m$ である. ここで累積分布関数は

$$F_W(w)=2-\frac{2}{1+w}$$

したがって

$$2-\frac{2}{1+m}=\frac{1}{2}.$$

これを解いて

$$m=\frac{1}{3}.$$

参考文献

日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]

日本統計学会

過去問2012年・2013年

Amazonで見る

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る