2013年 統計数理 問4

日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]

日本統計学会

過去問2012年・2013年

Amazonで見る

解説

ウィルコクソンの符号順位検定に関する問題です.
問題文は一見難しそうですが、一つずつ整理すると簡単な確率の問題に帰着できます.

問題設定として以下の条件があります.

• 2変量連続型分布からの無作為標本 $(x_1,y_1),\dots ,(x_n,y_n)$
• 差 $z_i=y_i-x_i$
• 差　$z_i$ の母集団分布 $F(z)$の中央値を $\theta$
• $H_0:\theta =0$ vs $H_1:\theta >0$
• 有意水準5%の検定
• $\theta$を中心に左右対称
• $\mathrm{\forall }i\in \{1,\dots ,n\},z_i\ne 0.$
• $\mathrm{\forall }i\ne j\in \{1,\dots ,n\},|z_i|\ne |z_j|$
• 棄却限界値を $c$ として $T^{+}=\sum _{z_i>0}{R}_i>0\Rightarrow \text{Reject}$

[1] サンプルサイズ

解説

すべての $z_i$ が正でもサンプルサイズ $n$ によって検定で有意にならない.

つまり
すべての $z_i$ が正でも $H_0$ を棄却できない.

$H_0$を棄却できるためには $n$はいくつ以上するか, という問題です.

解答

$H_0$ のもとでは, $z_i$が正になる確率は $\frac{1}{2}$である.
したがって有意確率 $p=1\times (\frac{1}{2}{)}^n>0.05$ のときは棄却できない.
(当たり前だが、$z_i$ がすべて正になるのは1通り)

$n$ と有意確率の値を表でまとめると,

n	$p=(1/2{)}^n$	判定(有意水準5%)
1	0.50000	Accept
2	0.25000	Accept
3	0.12500	Accept
4	0.06250	Accept
5	0.03125	Reject
6	0.01563	Reject

したがって $n$ は $5$ 以上

[2] 棄却限界値と有意確率

解説

おそらく[2]がこの問で一番大変だと思います.
数え上げは必ず見直しをしたいですね.

横軸を順位和, 縦軸にcountをとったときのヒストグラムと分布は以下のようになります.

このとき, 右側確率が5%を超えるような順位和が棄却限界値となります.

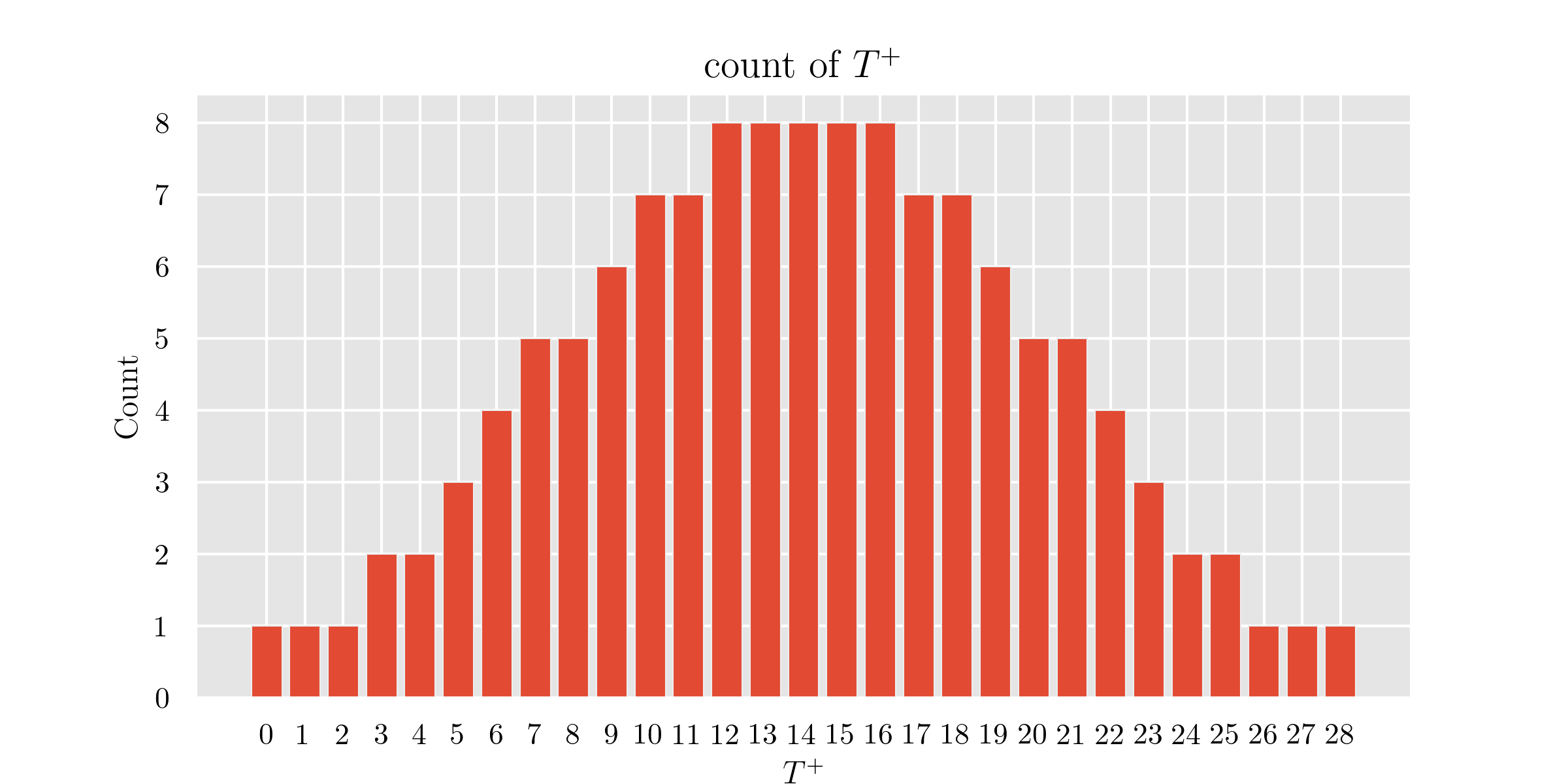
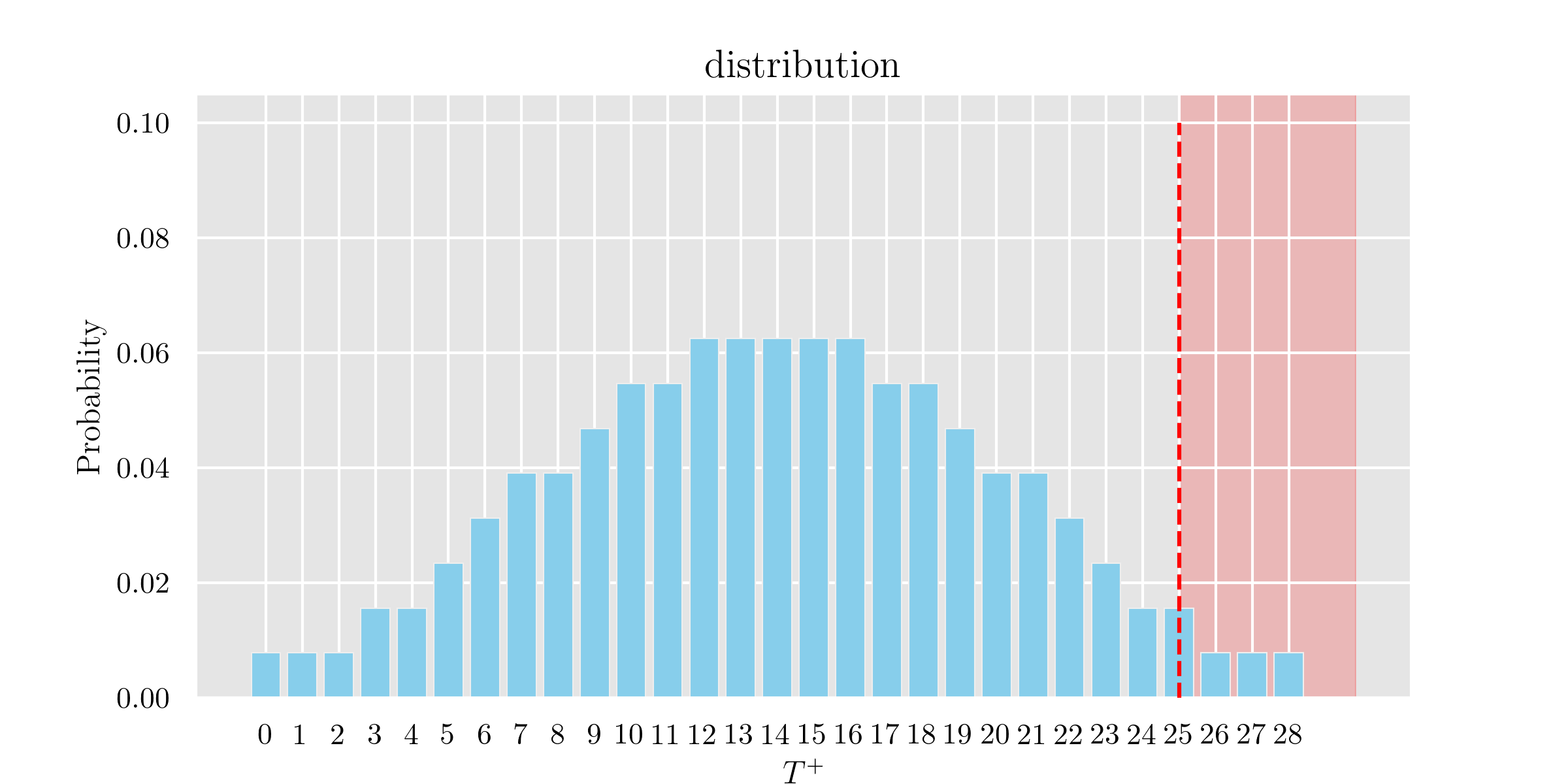
解答

$n=7$ のとき（差0なし・同順位なし）$T^{+}$ の値は $T^{+}\in \{0,\dots ,28\}$.

$T^{+}$	組み合わせ例	組み合わせ数	右側累積個数	右側確率 $p$
28	$\{1,2,3,4,5,6,7\}$	1	1	$1/128=0.00781$
27	$\{2,3,4,5,6,7\}$	1	2	$2/128=0.0156$
26	$\{1,3,4,5,6,7\}$	1	3	$3/128=0.0234$
25	$\{3,4,5,6,7\},\{1,2,4,5,6,7\}$	2	5	$5/128=0.0391$
24	$\{2,4,5,6,7\},\{1,2,3,5,6,7\}$	2	7	$7/128=0.0547$

よって $Pr(T^{+}\ge c)\le 0.05$ を満たす最小の棄却点は $c=25$.
実際の有意確率は $5/128\approx 0.0391$.

[3] 期待値と分散

解説

同順位なし, 差0が無い場合, $I_i$ は独立に $\mathrm{Bern}(p)$ に従う確率変数 $I_i$ を用いて以下のように変形できます.

$$\begin{array}{rl}{T}^{+}& =\sum _{z_i>0}{R}_i\\ & =\sum _{i=1}^n{R}_i{I}_i\end{array}$$

ベルヌーイ分布を用いることで、全ての順位を同時に扱え、計算の見通しが良くなります.

期待値

$$\begin{array}{rl}\mathbb{E}[T^{+}]& =\mathbb{E}\left[\sum _{i=1}^n{R}_i{I}_i\right]\\ & =\sum _{i=1}^n{R}_i\mathbb{E}[I_i]\\ & =\sum _{i=1}^n{R}_{i}p\\ & =\frac{n(n+1)}{2}p\end{array}$$

$H_0$ で $p=\frac{1}{2}$ より

$$\mathbb{E}[T^{+}]=\frac{n(n+1)}{4}$$

分散

$$\begin{array}{rl}\text{V}[T^{+}]& =\text{V}\left[\sum _{i=1}^n{R}_i{I}_i\right]\\ & =\sum _{i=1}^n{R}_i^2\text{V}[I_i]\\ & =p(1-p)\sum _{i=1}^n{R}_i^2\\ & =p(1-p)\frac{n(n+1)(2n+1)}{6}\end{array}$$

$H_0$ では,

$$\text{V}[T^{+}]={\displaystyle \frac{n(n+1)(2n+1)}{24}}$$

[4] 正規近似　棄却域

解説

正規近似（連続修正無し）
$n=7$ のとき,

$$\begin{array}{rl}\mu & =\frac{n(n+1)}{4}=14,\\ \sigma & =\sqrt{\frac{n(n+1)(2n+1)}{24}}=\sqrt{35},\\ T^{+}& \sim \mathcal{N}(14,\sqrt{35})\end{array}$$

解答

標準化すると,

$$Z=\frac{T^{+}-\mu }{\sigma }\sim \mathcal{N}(0,1)$$

したがって棄却域は,

$$\begin{array}{rl}Z& >1.645\\ \iff \frac{T^{+}-\mu }{\sigma }& >1.645\\ \iff T^{+}& >\mu +1.645\sigma \\ & =14+1.645\sqrt{35}\\ & =23.73\end{array}$$$$\begin{array}{r}{T}^{+}\ge 24\end{array}$$

解説

正規近似（連続修正あり）
$n=7$ のとき,

$$\begin{array}{rl}{T}^{+}& \sim \mathcal{N}(14+\frac{1}{2},\sqrt{35})\end{array}$$

連続修正（半整数補正）とは？

---

離散型分布の正規近似

解答

標準化すると,

$$Z=\frac{T^{+}-\mu -0.5}{\sigma }\sim \mathcal{N}(0,1)$$

したがって棄却域は,

$$\begin{array}{rl}Z& >1.645\\ \iff \frac{T^{+}-\mu -0.5}{\sigma }& >1.645\\ T^{+}& \ge \mu +1.645\sigma +0.5\\ & =14+1.645\sqrt{35}+0.5\\ & =24.23\end{array}$$$$\begin{array}{r}{T}^{+}\ge 25\end{array}$$

これは厳密分布の棄却域 $T^{+}\ge 25$ と一致する.

参考文献

日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]

日本統計学会

過去問2012年・2013年

Amazonで見る

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る