2013年統計数理問3

Takeda Katsuji2025/09/25約3分

2013年統計数理問3

日本統計学会公式認定統計検定 1級公式問題集[2012〜2013年]
日本統計学会
過去問2012年・2013年
Amazonで見る

解説

二項分布の基本的な性質を問われる問題です.
期待値, 分散, 不偏推定量, 最尤推定量([1]~[3])は完璧に導出できるようにしたいです.

[1] 期待値と分散

二項分布の期待値と分散

二項分布の記事をご覧ください.

[2] 最尤推定量と不偏推定量

$\hat{p} = \frac{X}{n}$ が最尤推定量かつ不偏推定量であることを示す.

最尤推定量

解答

$X \sim Binomial (n, p)$ の尤度は

L (p; X) =_{n} C_{x} p^{x} (1 - p)^{n - x} (0 \leq p \leq 1)

対数尤度は

\begin{aligned} ℓ (p) & = \log L \\ = \log (_{n} C_{x}) + x \log p + (n - x) \log (1 - p) \end{aligned}

微分してゼロに置く:

ℓ^{'} (p) = \frac{x}{p} - \frac{n - x}{1 - p} = 0 \Rightarrow \hat{p} = \frac{x}{n}

したがって $\hat{p} = \frac{X}{n}$ は最尤推定量である.

不偏推定量

解答

\begin{aligned} E [\frac{X}{n}] & = \frac{1}{n} E [X] \\ = \frac{1}{n} n p \\ = p \end{aligned}

したがって $\hat{p} = X / n$ は不偏推定量である.

分散の不変推定量

解答

$\hat{p}$ の分散 $w_{n} (p)$ は,

\begin{aligned} w_{n} (p) & = V [\hat{p}] \\ = V [\frac{X}{n}] \\ = \frac{1}{n^{2}} V [X] \\ = \frac{1}{n^{2}} n p (1 - p) \\ = \frac{p (1 - p)}{n} \end{aligned}

$w_{n} (p)$ 推定量 $\hat{w_{n}} = w_{n} (\hat{p})$ より,

\begin{aligned} w_{n} (\hat{p}) & = \frac{\hat{p} (1 - \hat{p})}{n} \end{aligned}

推定量 ${\hat{w}}_{n} = w_{n} (\hat{p})$ が不偏推定量でないことを確認する.

\begin{aligned} E [w_{n} (\hat{p})] & = E [\frac{\hat{p} (1 - \hat{p})}{n}] \\ = \frac{1}{n} E [\frac{X}{n} (1 - \frac{X}{n})] \\ = \frac{1}{n} E [\frac{X}{n} - \frac{X^{2}}{n^{2}}] \\ = \frac{1}{n^{2}} E [X - \frac{X^{2}}{n}] \\ = \frac{1}{n^{2}} (E [X] - \frac{1}{n} E [X^{2}]) \end{aligned}

ここで期待値と二次モーメントより(二項分布の性質)

\begin{aligned} E [X] & = n p \\ E [X^{2}] & = n (n - 1) p^{2} + n p \end{aligned}

より

\begin{aligned} E [w_{n} (\hat{p})] & = \frac{1}{n^{2}} (E [X] - \frac{1}{n} E [X^{2}]) \\ = \frac{1}{n^{2}} (n p - \frac{1}{n} (n (n - 1) p^{2} + n p)) \\ = \frac{1}{n^{2}} (n p - (n - 1) p^{2} - p) \\ = \frac{1}{n^{2}} (n p - n p^{2} + p^{2} - p) \\ = \frac{(n - 1) p (1 - p)}{n^{2}} \\ = \frac{n - 1}{n} \times \frac{p (1 - p)}{n} \\ = \frac{n - 1}{n} w_{n} (p) \end{aligned}

したがって $w_{n} (\hat{p})$ は不偏推定量ではない.

また上式から

$E [\frac{n}{n - 1} w_{n} (\hat{p})]$ は不偏推定量となるので

{\tilde{w}}_{n} = c (n) {\hat{w}}_{n}

を満たす $c (n)$ は

c (n) = \frac{n}{n - 1}

[4] 被覆確率

正規近似のWald区間で比較する.

${\hat{w}}_{n}$ 信頼区間の大きさ $| C I ({\hat{w}}_{n}) |$ は,

\begin{aligned} | C I ({\hat{w}}_{n}) | & = (\hat{p} + 1.96 \sqrt{{\hat{w}}_{n}}) - (\hat{p} - 1.96 \sqrt{{\hat{w}}_{n}}) \\ = 2 \times 1.96 \sqrt{{\hat{w}}_{n}} \end{aligned}

${\tilde{w}}_{n}$ 信頼区間の長さ $| C I ({\tilde{w}}_{n}) |$ は,

\begin{aligned} | C I ({\tilde{w}}_{n}) | & = (\hat{p} + 1.96 \sqrt{{\tilde{w}}_{n}}) - (\hat{p} - 1.96 \sqrt{{\tilde{w}}_{n}}) \\ = 2 \times 1.96 \sqrt{{\tilde{w}}_{n}} \\ = 2 \times 1.96 \sqrt{\frac{n}{n - 1}} \sqrt{{\hat{w}}_{n}} \end{aligned}

この二つの区間を比べると

| C I ({\tilde{w}}_{n}) | > | C I ({\hat{w}}_{n}) |

であることが分かる.

信頼区間と被覆確率

信頼区間とは，データ $X$ から区間推定量 $C I (X)$ を構成し，同じ手順を多数回繰り返すと，真のパラメータ $θ$ がその区間に含まれる割合が信頼係数 $1 - α$ になるよう設計された区間のことを指す.

例えば, 信頼係数を95%で構成するとき, 100回実験をすれば95回は信頼区間にパラメータ $θ$ が含まれているということです.

被覆確率とは，真の値 $θ$ の下で区間が $θ$ を含む確率

Coverage (θ) = P_{θ} (θ \in C I (X))

のこと. 理想的には $Coverage (θ) = 1 - α$ だが，有限標本や近端領域では

Coverage (θ) \neq 1 - α

となる場合があるため，実際の被覆（実被覆）をシミュレーション等で評価するのが実務的です.

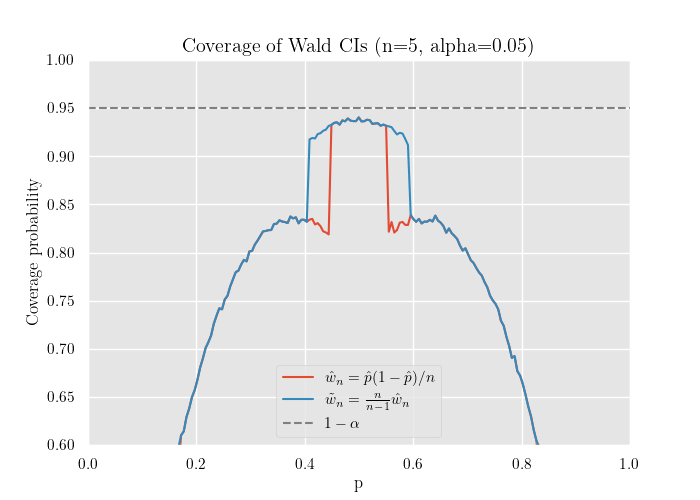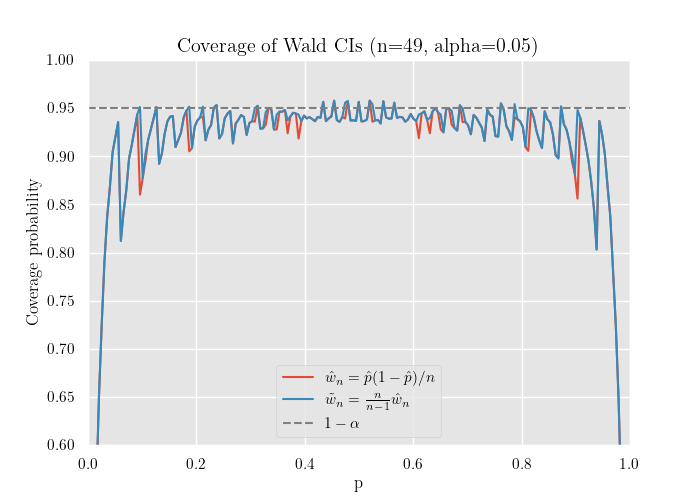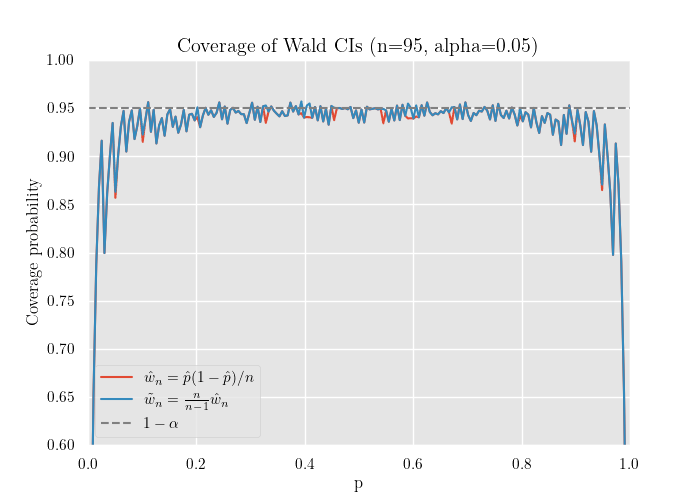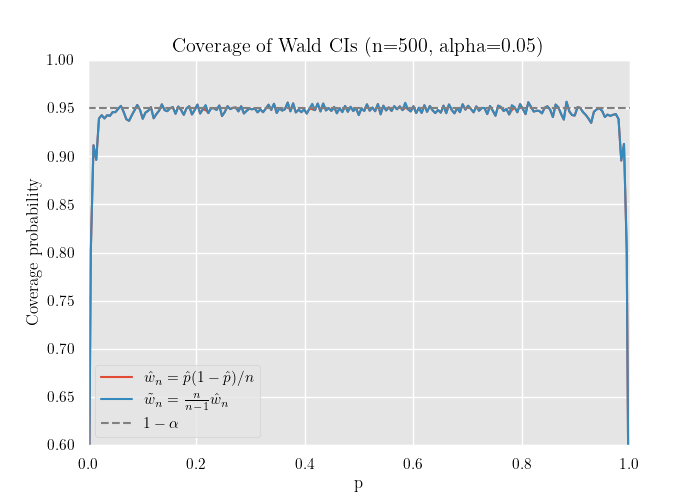
シミュレーション

赤が補正前の推定量 ${\hat{w}}_{n}$ , 青が補正後の推定量 ${\tilde{w}}_{n}$ です.
グラフから, 青の線の方が名目 $0.95$ （信頼係数 $95 %$ ）に近いことが分かります.

また, $p = 0, 1$ 付近では被覆確率が極端に低下し, 標本数が小さいと $p$ 全域で $95 %$ を下回ることが確認できます.

まとめ

離散母数問題でのWald区間は, 被覆確率を名目値に一致させるには十分な標本数が必要となる.
実務では Wilson や Clopper–Pearson の正確区間などの代替や補正を検討する.

2013年統計数理問3

2013年統計数理問3

日本統計学会公式認定統計検定 1級公式問題集[2012〜2013年]

[1] 期待値と分散

[2] 最尤推定量と不偏推定量

最尤推定量

不偏推定量

分散の不変推定量

[4] 被覆確率

参考文献

日本統計学会公式認定統計検定 1級公式問題集[2012〜2013年]

増訂版日本統計学会公式認定統計検定１級対応統計学

新装改訂版　現代数理統計学

2013年 統計数理 問3

2013年統計数理問3