半整数補正

半整数補正とは二項分布などの離散型分布を正規近似で連続型の分布に近似するときに近似精度を上げる方法です.
この記事ではグラフやアニメーションとともに、この近似がどの程度有効か議論していきたいと思います.

解説

二項分布 $X\sim \mathrm{Bin}(n,p)$ の正規近似は

$$\begin{array}{r}X\sim \mathcal{N}(np,np(1-p))\end{array}$$

今回 $\mathrm{Pr}(X\le c)$ の値を

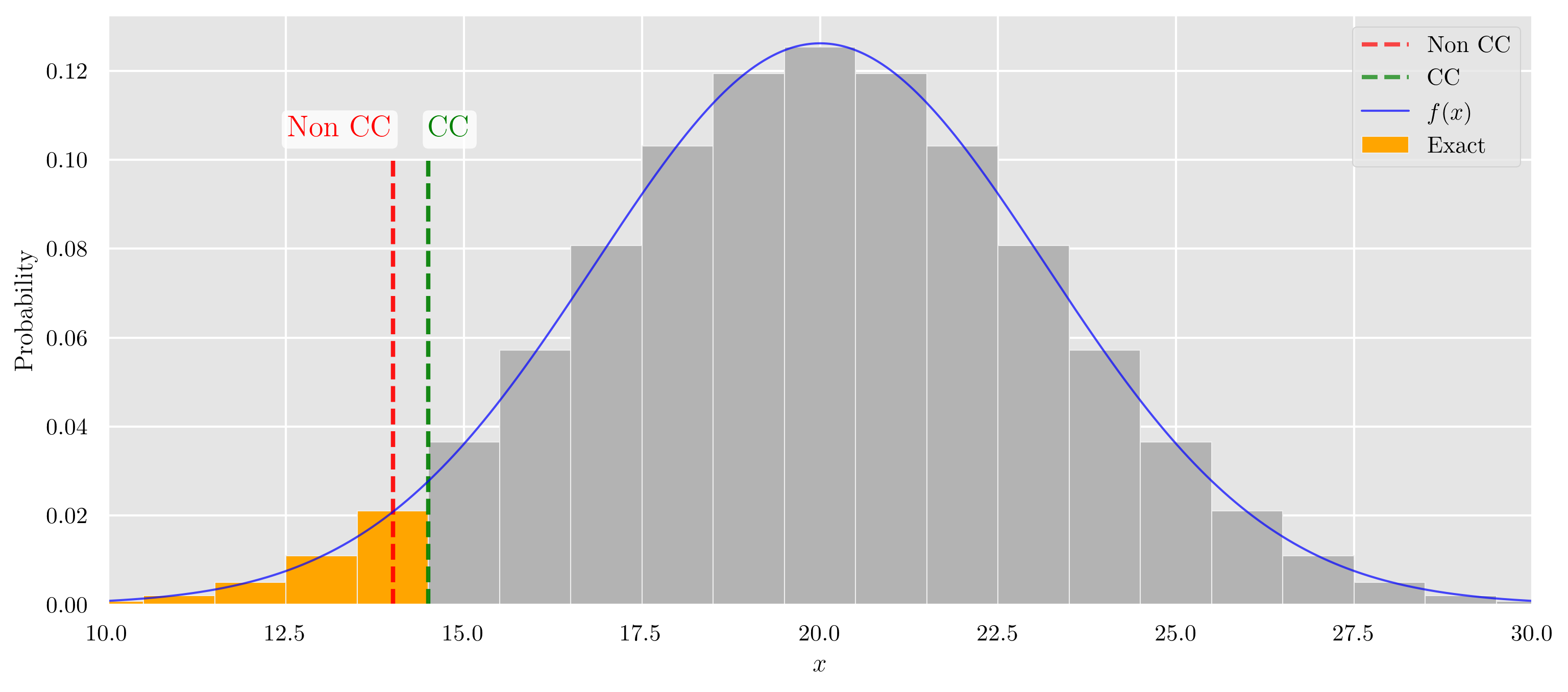
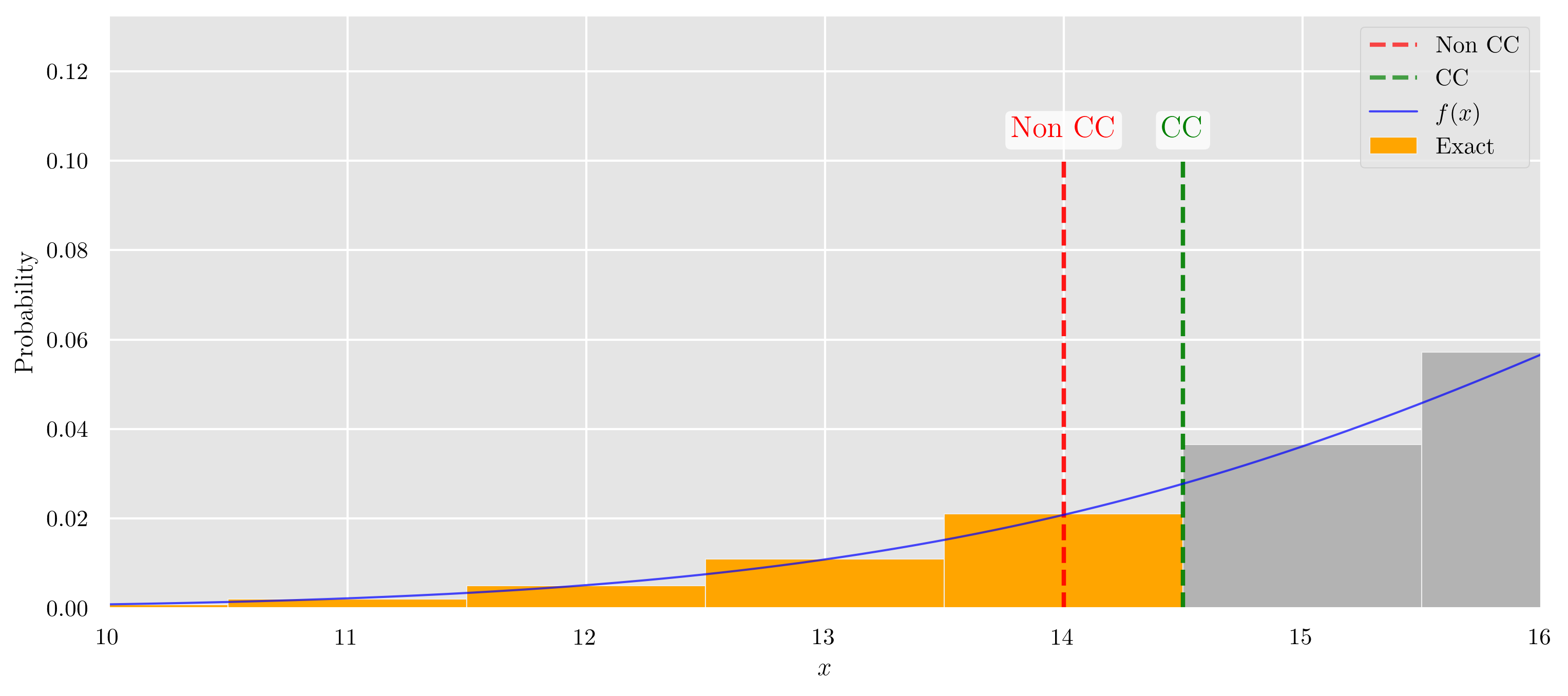
• 正確確率(Exact) オレンジ色の長方形の面積の和
• 正規近似・半整数補正なし(Non CC) 赤色の線より左側の曲線下面積
• 正規近似・半整数補正あり(CC) 緑色の線より左側の曲線下面積

この3種類値を比較していきます.

3種類の面積のグラフ

Exactとの差のアニメーション1

設定

二項分布の 確率 $p$ を固定して $n$ を増加 してExactとの差分をプロットします.

• 分布: $X\sim \mathrm{Bin}(n,p)$（$p=0.5$）
• 片側: 左片側（$Pr(X\le c)$）
• しきい値: $c=\lfloor an\rfloor$（本文では $a=0.35$）
• $n$ の範囲: $n_{min}=10,n_{max}=100$

解説

標準正規分布の分布関数を $\mathrm{\Phi }$ とし，$\mu =np,\sigma =\sqrt{np(1-p)}$ とする.

• Exact のとき

$$Pr(X\le c)=\sum _{k=0}^c(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}.$$

• 補正なしのとき

$$Pr(X\le c{)}_{NonCC}\approx \mathrm{\Phi }\left(\frac{c-\mu }{\sigma }\right).$$

• 半整数補正ありのとき

$$Pr(X\le c{)}_{CC}\approx \mathrm{\Phi }\left(\frac{c+\frac{1}{2}-\mu }{\sigma }\right).$$

差の可視化は

$$\begin{array}{rl}{\mathrm{\Delta }}_{\text{Non CC}}(n)& =\mathrm{\Phi }\left(\frac{c-\mu }{\sigma }\right)-Pr(X\le c)\\ {\mathrm{\Delta }}_{\text{CC}}(n)& =\mathrm{\Phi }\left(\frac{c+\frac{1}{2}-\mu }{\sigma }\right)-Pr(X\le c).\end{array}$$

Non CC と CC で Exact との差をプロットすると以下になる.

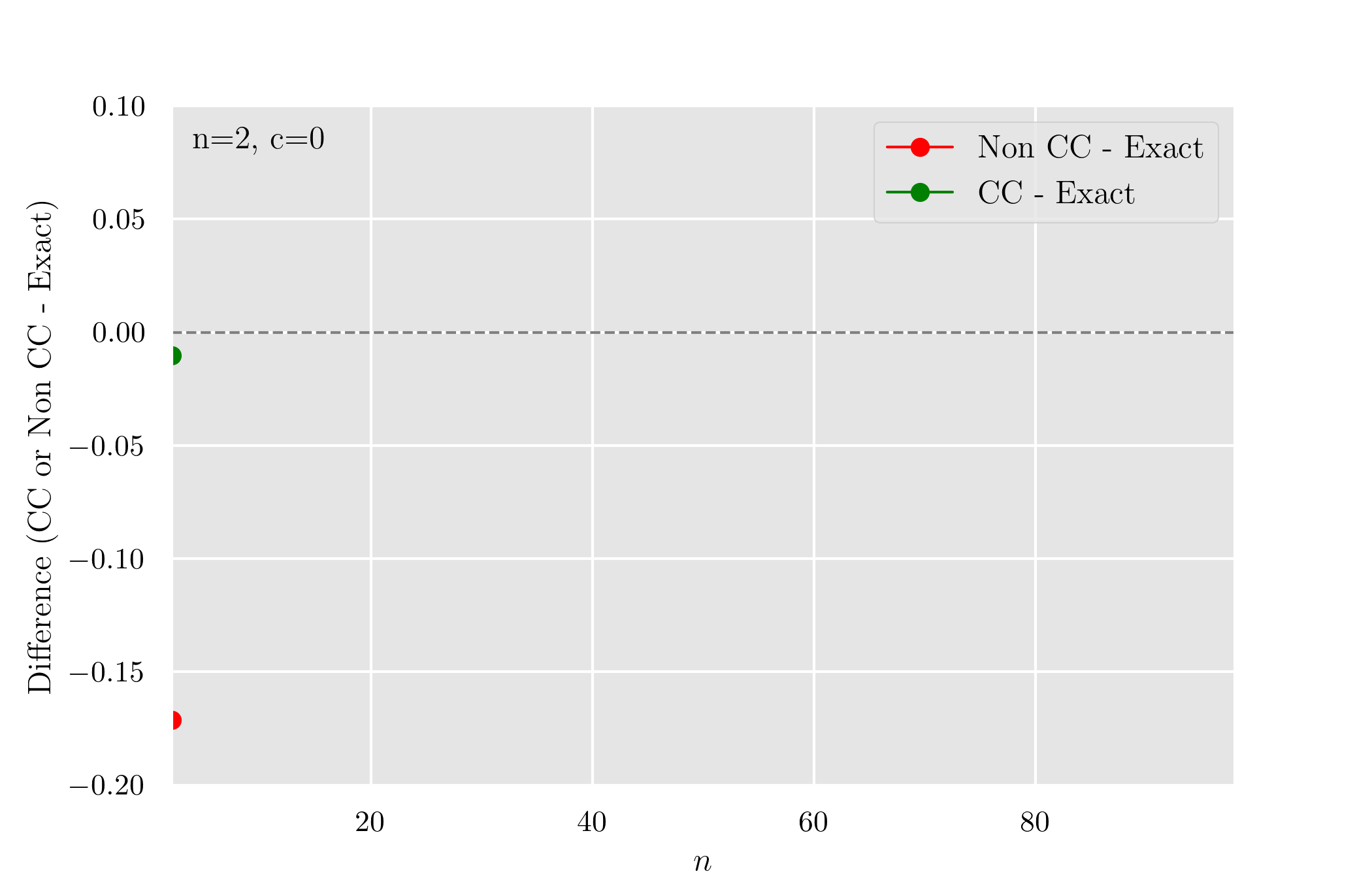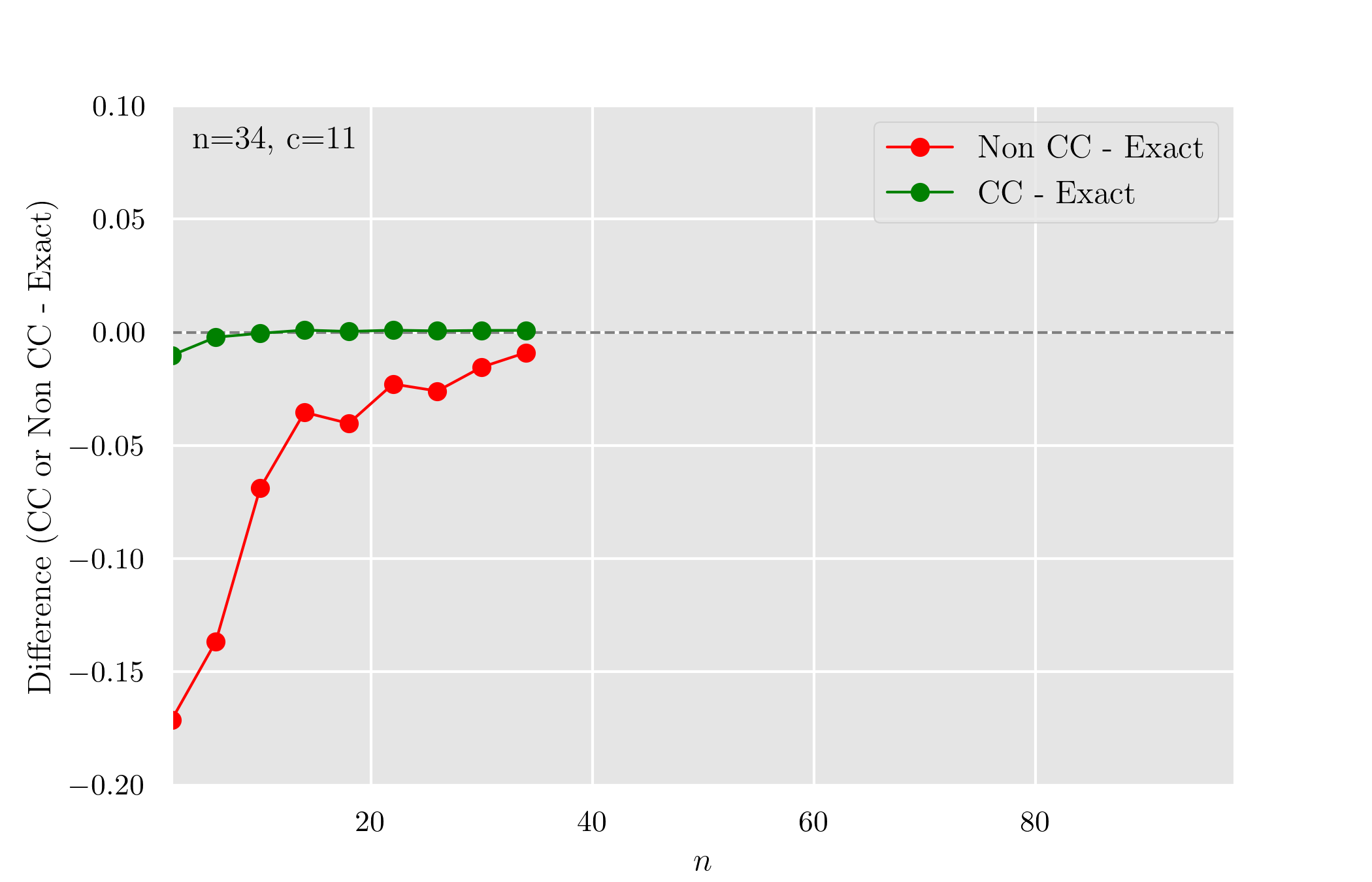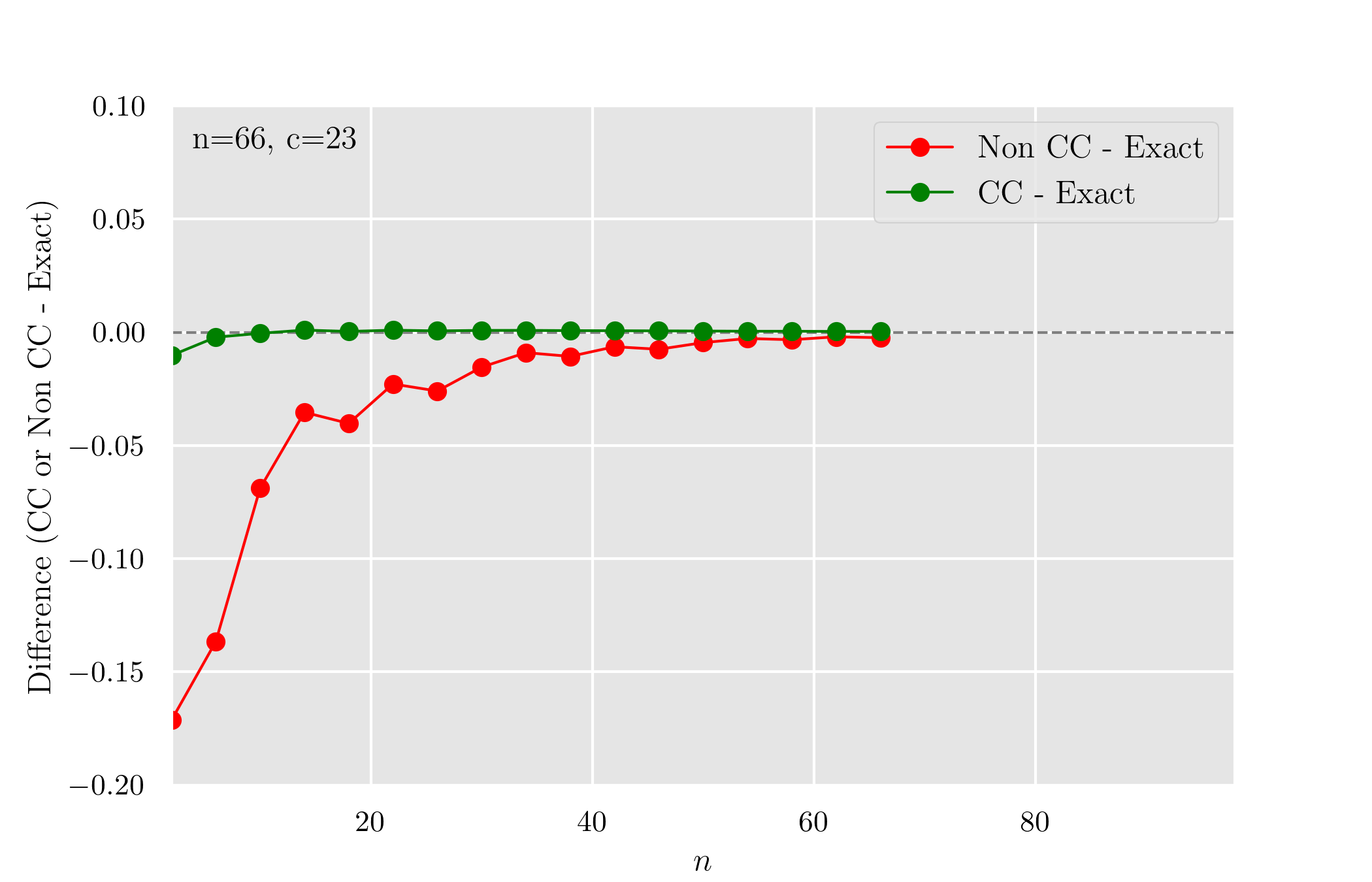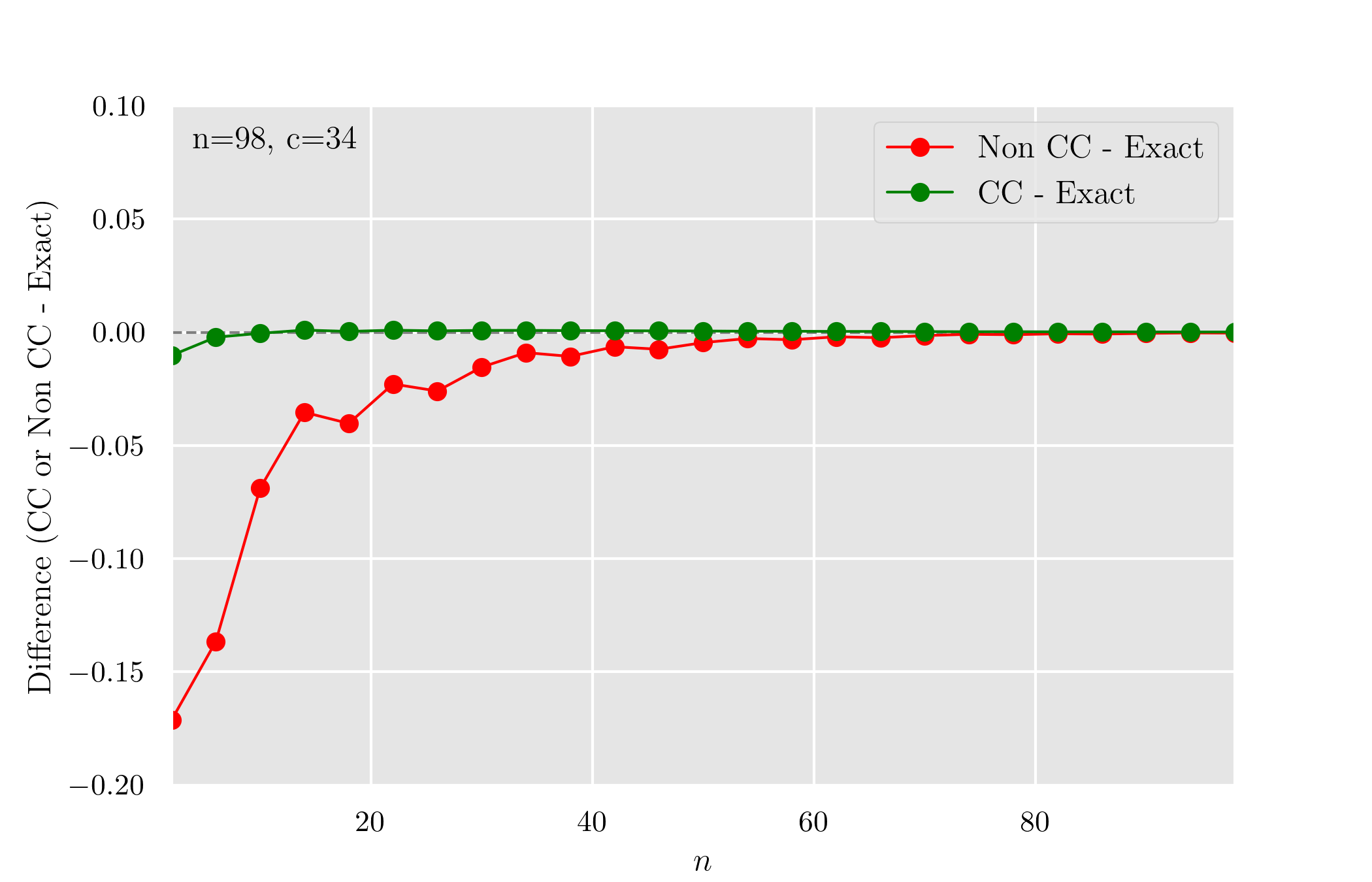
まとめ

左片側では小さな $n$ で ${\mathrm{\Delta }}_{\text{Non CC}}<0$（過少推定）になりやすい傾向にあります.
一方で 半整数補正は小さな $n$ でも差を大きく縮めている ことがわかります.

Exactとの差のアニメーション2

設定

二項分布の 確率 $n$ を固定して $p$ を増加 してExactとの差分をプロットします.

• 分布: $X\sim \mathrm{Bin}(n,p)$ ($n=50$)
• 片側: 左片側（$Pr(X\le c)$）
• しきい値: $c=\lfloor an\rfloor$（本文では $a=0.35$）
• $p$ の範囲: $p_{min}=0,p_{max}=1$

解説

$n=50$で固定し, $p\in [0,1]$ の範囲で動かす,
Non CC と CC で Exact との差をプロットすると以下になる.

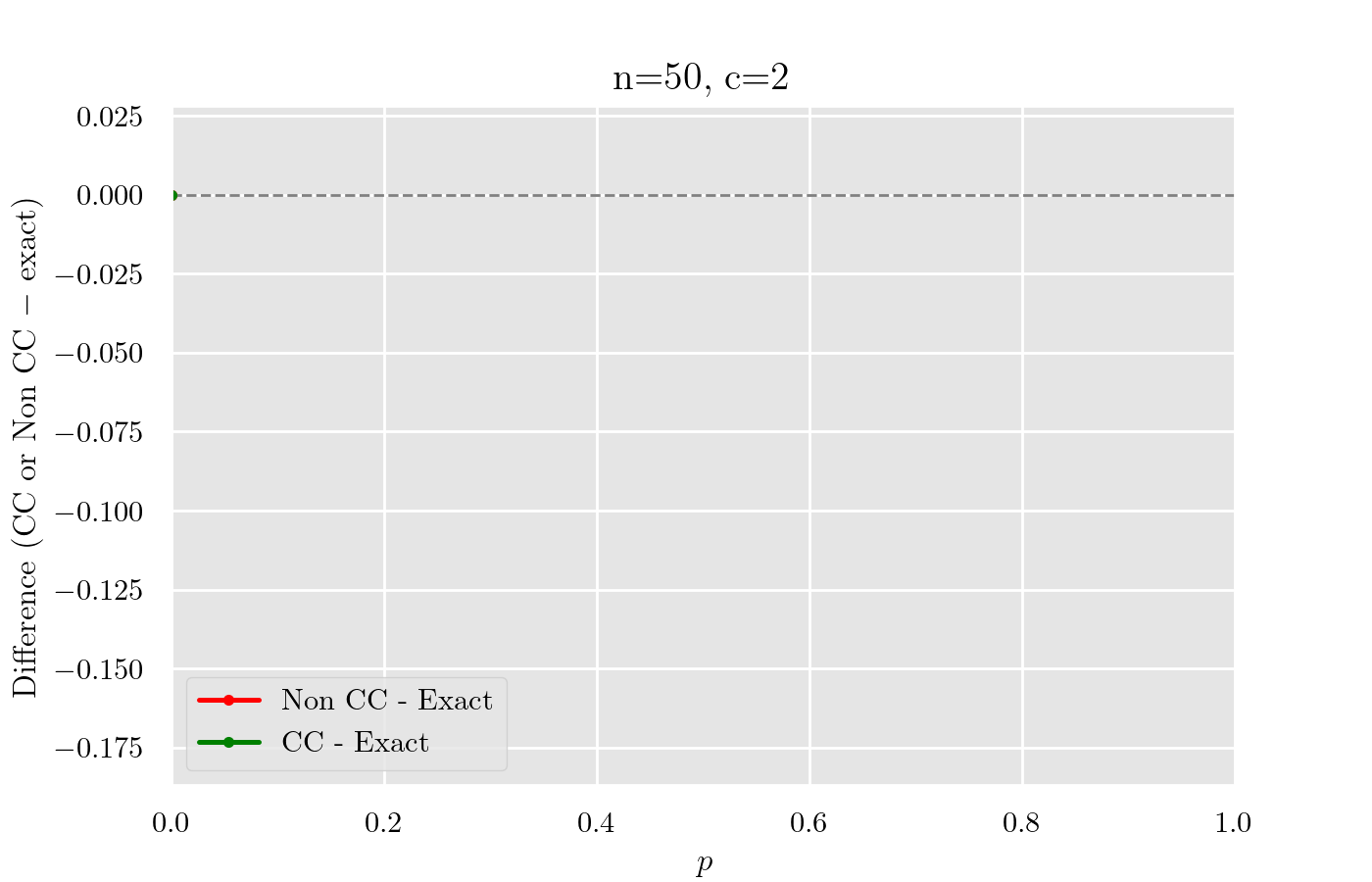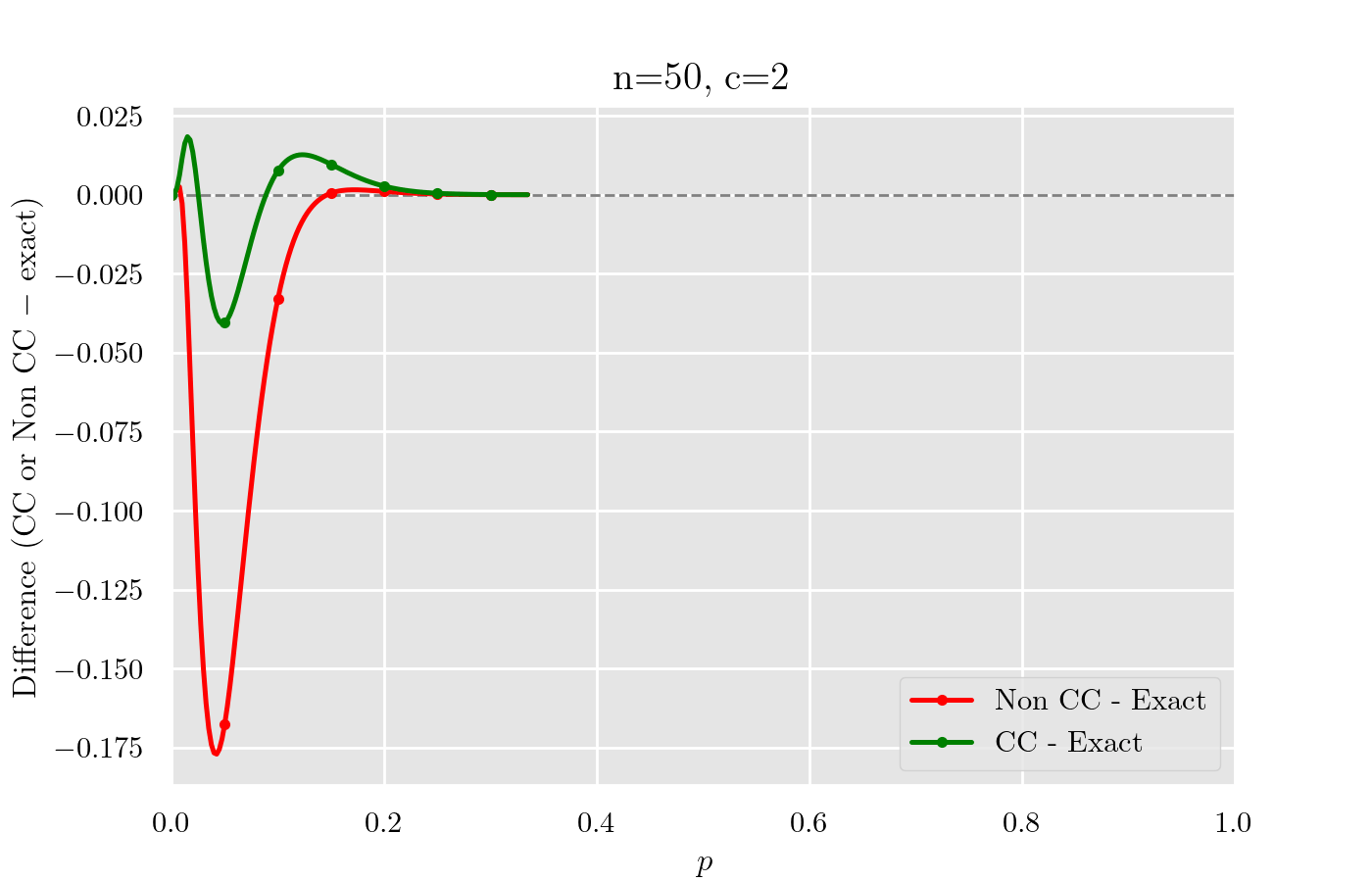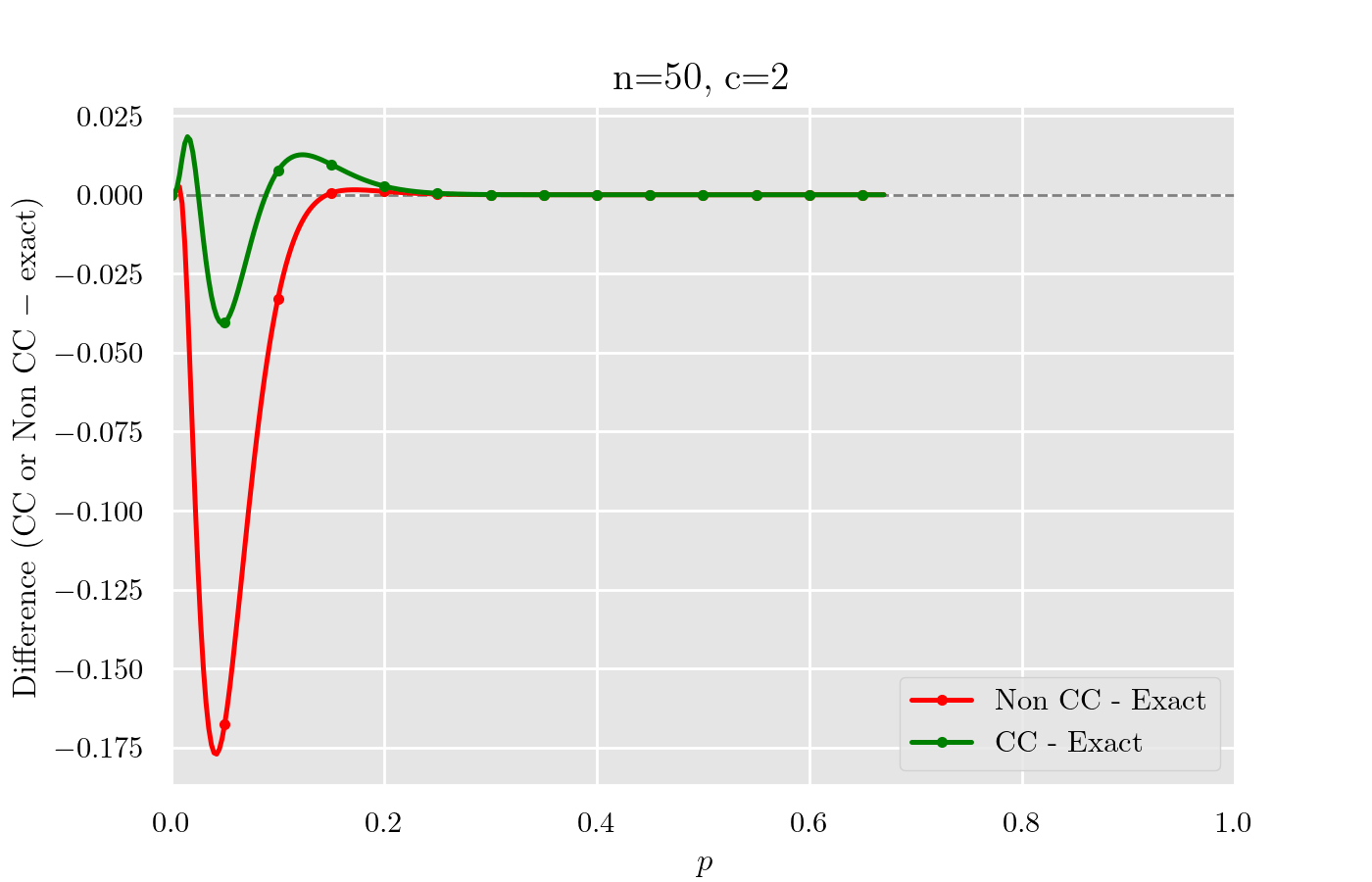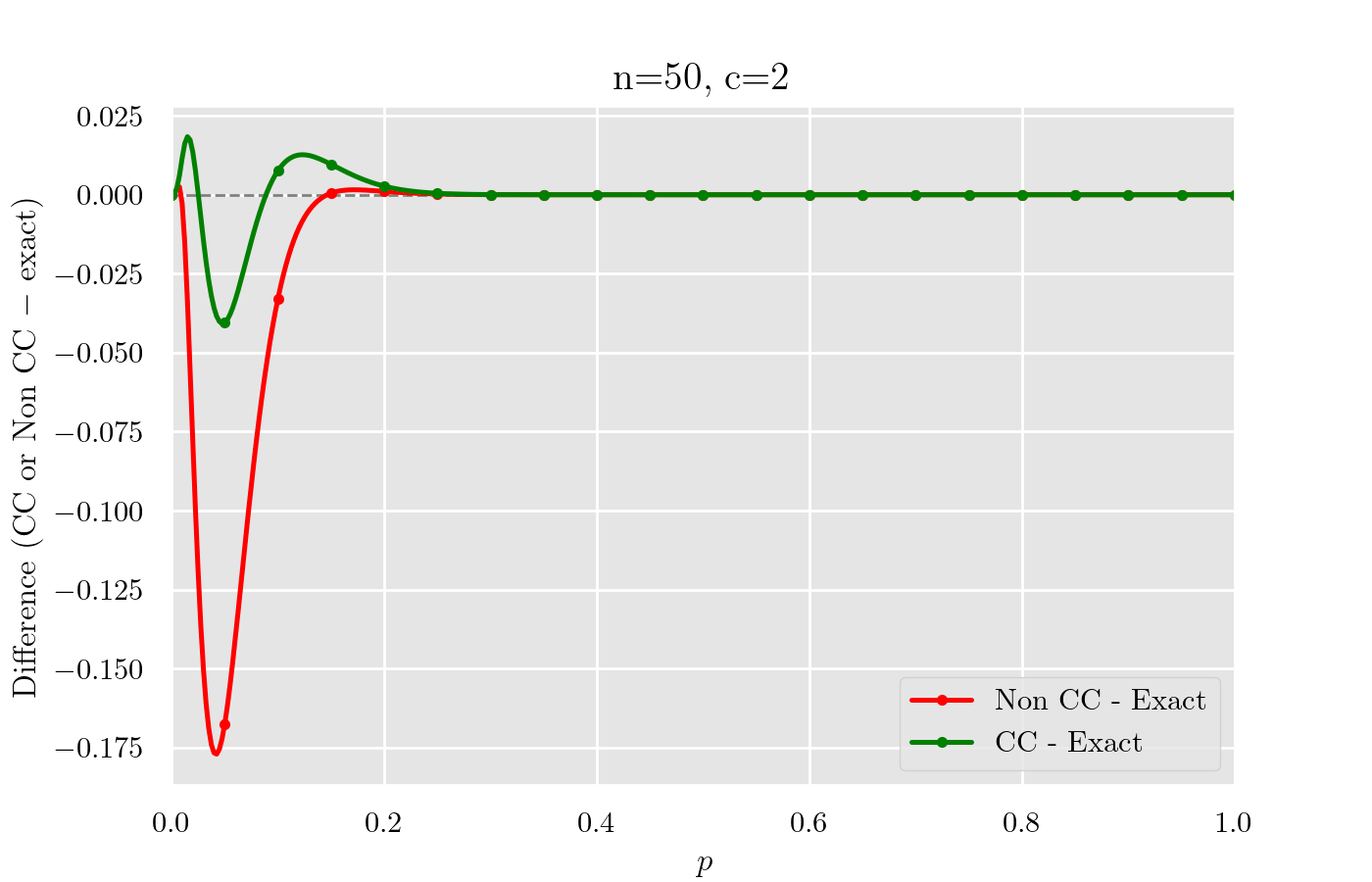
まとめ

• 本稿では $n=50$ を固定し，$p$ を $[0,1]$ で動かして左片側 $Pr(X\le c)$ の近似誤差を比較しました．
• 近似なし（Non CC）は，$\mu =np$ が $c+\frac{1}{2}$ に近づく付近で誤差が最大化しやすいことを確認しました．
• 半整数補正（CC）は，この最大誤差点付近でも誤差を大きく抑えられることを示しました．
• 例として $c=2$ の設定では，誤差は $p=(c+\frac{1}{2})/n=0.05$ 付近で最大化しやすく，CC による改善が明瞭に観察できます．
• 実務では 半整数補正を利用するのをお勧めします.

参考文献

増訂版 日本統計学会公式認定 統計検定１級対応 統計学

日本統計学会

統計検定1級公式教本 網羅的に記述してあるので辞書的に使うことをおすすめします

Amazonで見る 楽天で見る

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る