2次元正規分布の条件付き分布

統計検定1級では2次元正規分布の条件付き分布がよく出てきます.

しかし公式を丸暗記しようとすると、平均や分散の形を間違えやすく、苦労する人も多いと思います.

そこで本記事では 「標準正規分布」から「一般の正規分布」へ変数変換する流れを押さえることで、

公式をシンプルに導出する手順をご紹介します.

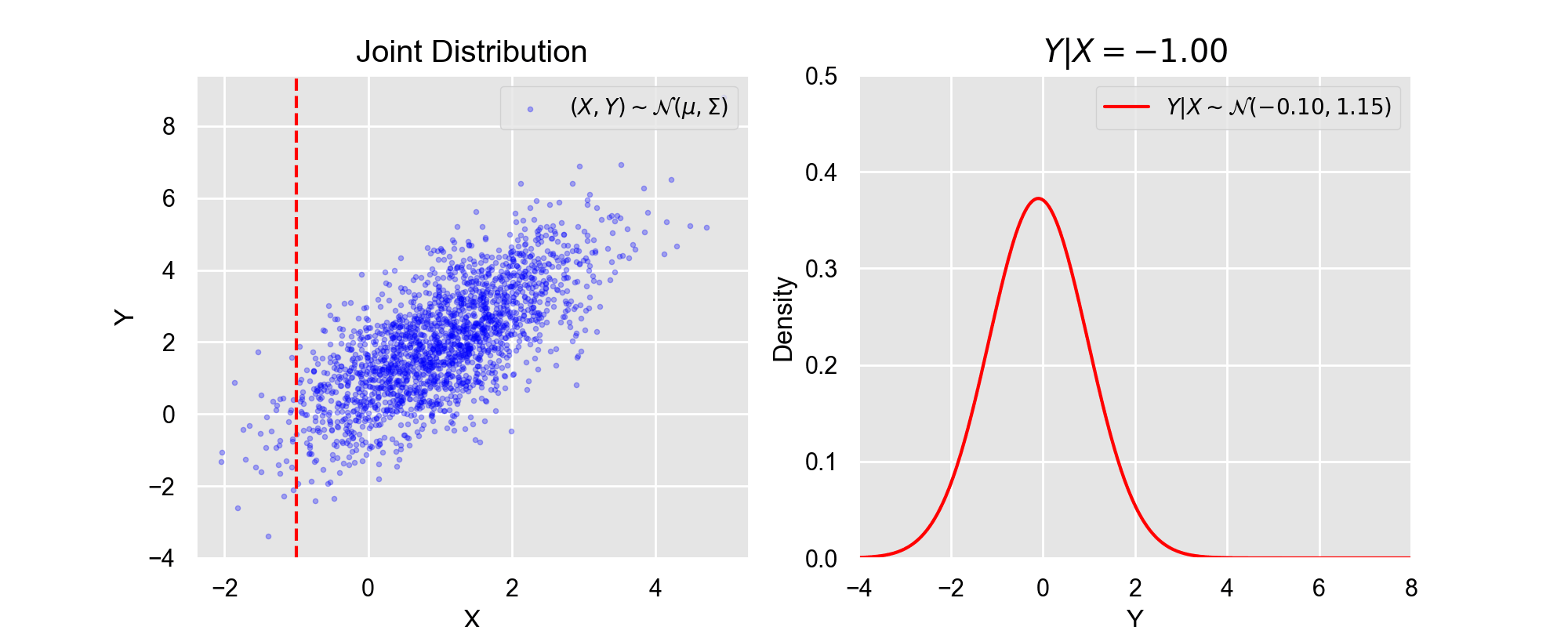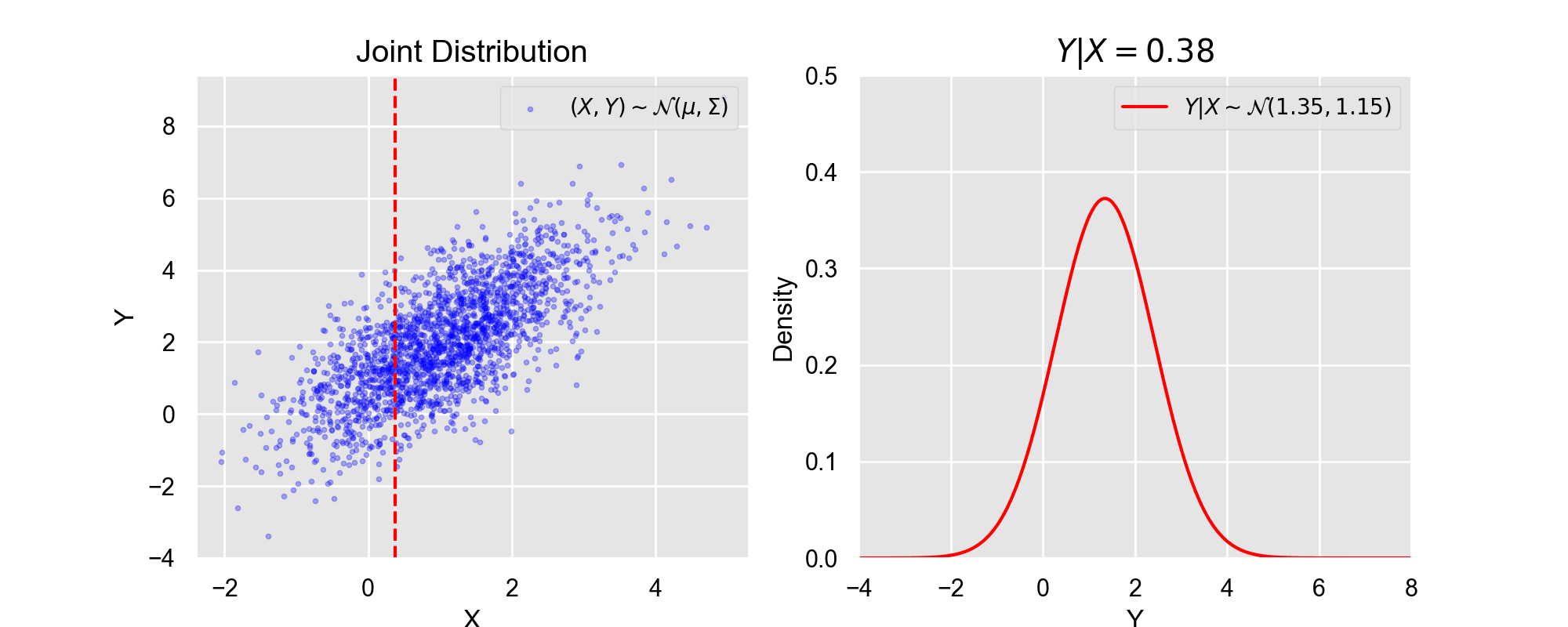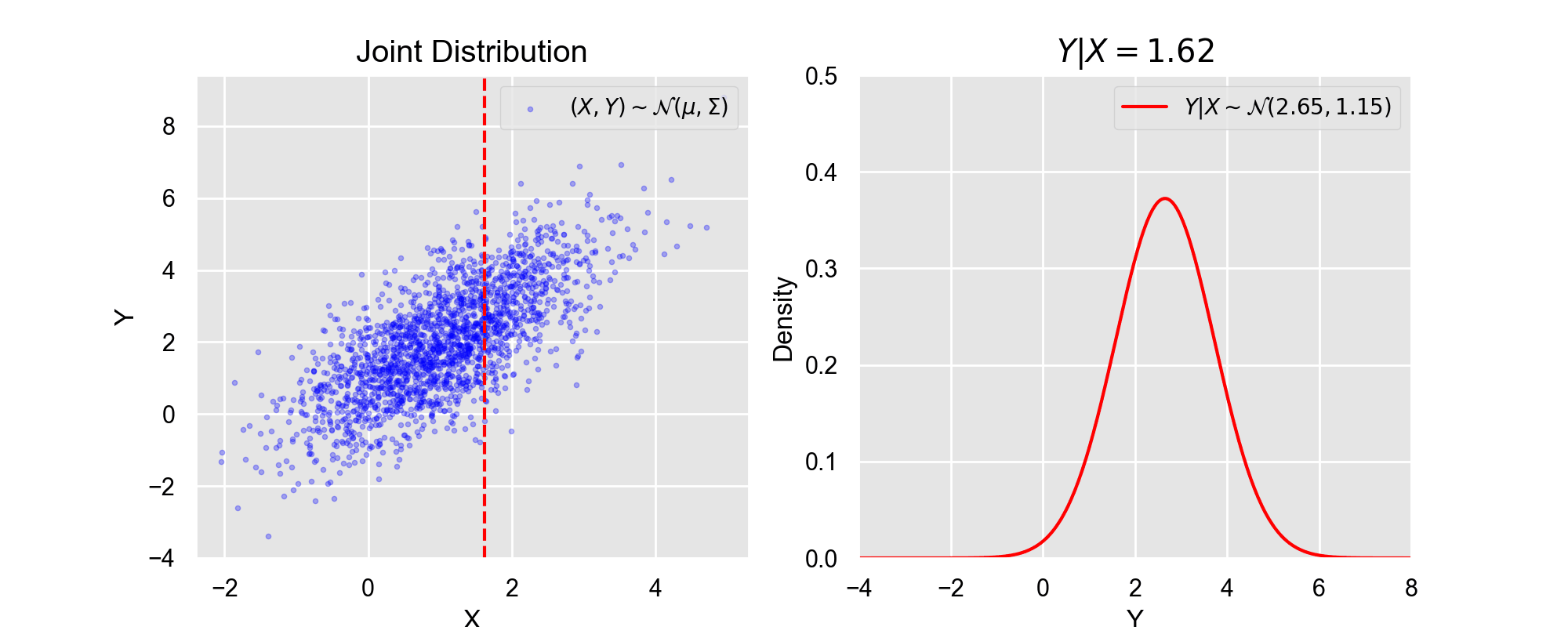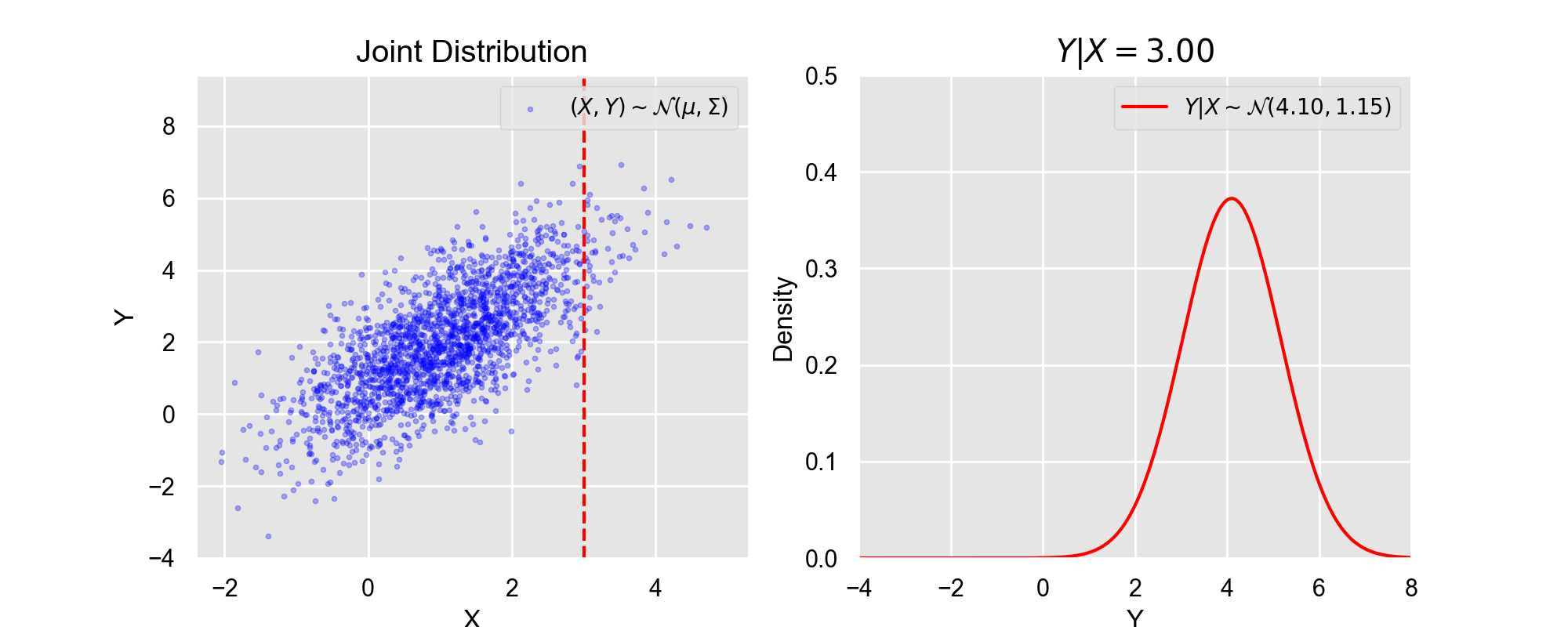
ポイント

• 標準正規分布での結果を 「そのままスケール・シフト」 するだけで一般形が出る
• 覚えるべきは「標準正規の条件付き分布」の形だけ

これを押さえると、統計検定の条件付き分布問題もスッキリ解けます！

1. $X,Y$ が標準正規分布の場合

$(X,Y)$ が平均ベクトル $\mathbf{0}$, 分散共分散行列

$$\mathrm{\Sigma }=\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right)$$

に従うとする：

$$(X,Y)\sim \mathcal{N}(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right))$$

条件付き分布

$X=x$ のときの $Y$ の条件付き分布は

$$Y\mid X=x\sim \mathcal{N}(\rho x,1-{\rho }^2)$$

導出の手順はこちら

導出

2次元正規分布の同時確率密度関数は

$$f(x,y)=\frac{1}{2\pi \sqrt{1-{\rho }^2}}\exp [-\frac{1}{2(1-{\rho }^2)}(x^2-2\rho xy+y^2)]$$

$X=x$ のときの条件付き分布は

$$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}$$

まず $X$ の周辺分布は $X\sim \mathcal{N}(0,1)$ なので

$$f_X(x)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2}$$

したがって

$$\begin{array}{rl}{f}_{Y|X}(y|x)& =\frac{{\displaystyle \frac{1}{2\pi \sqrt{1-{\rho }^2}}}\exp [-\frac{1}{2(1-{\rho }^2)}(x^2-2\rho xy+y^2)]}{{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-x^2/2}}\\ & =\frac{1}{\sqrt{2\pi (1-{\rho }^2)}}\exp \{-\frac{1}{2(1-{\rho }^2)}(y^2-2\rho xy+{\rho }^2{x}^2)\}\end{array}$$

指数の中を整理すると

$$y^2-2\rho xy+{\rho }^2{x}^2=(y-\rho x{)}^2$$

したがって

$$f_{Y|X}(y|x)=\frac{1}{\sqrt{2\pi (1-{\rho }^2)}}\exp (-\frac{(y-\rho x{)}^2}{2(1-{\rho }^2)})$$

これは平均 $\rho x$, 分散 $1-{\rho }^2$ の正規分布の密度関数である.

2. $X,Y$ が一般の正規分布の場合

標準正規分布からの変数変換を用いると，一般の場合も同様に導ける.

例えば

$$\begin{array}{rl}X& ={\mu }_X+{\sigma }_X{Z}_X,\\ Y& ={\mu }_Y+{\sigma }_Y{Z}_Y,\end{array}$$

ただし $(Z_X,Z_Y)$ が相関係数 $\rho$ を持つ標準2次元正規に従うとする.

このとき $(X,Y)$ は

$$(X,Y)\sim \mathcal{N}(\left(\begin{array}{c}{\mu }_X\\ {\mu }_Y\end{array}\right),\left(\begin{array}{cc}{\sigma }_X^2& \rho {\sigma }_X{\sigma }_Y\\ \rho {\sigma }_X{\sigma }_Y& {\sigma }_Y^2\end{array}\right))$$

条件付き分布

$X=x$ のときの $Y$ の条件付き分布は

$$Y\mid X=x\sim \mathcal{N}({\mu }_Y+\rho \frac{{\sigma }_Y}{{\sigma }_X}(x-{\mu }_X),{\sigma }_Y^2(1-{\rho }^2))$$

導出の手順はこちら

導出

1. 標準化
   標準化した変数を

$$Z_X=\frac{X-{\mu }_X}{{\sigma }_X},Z_Y=\frac{Y-{\mu }_Y}{{\sigma }_Y}$$

とすると，$(Z_X,Z_Y)$ は標準正規ベクトルで相関係数 $\rho$ を持つ：

$$(Z_X,Z_Y)\sim \mathcal{N}(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right))$$

2. 標準正規の場合の条件付き分布
   すでに導出した結果より

$$Z_Y\mid Z_X=z_x\sim \mathcal{N}(\rho z_x,1-{\rho }^2)$$

3. 元の変数に戻す
   $X=x$ に対応する $Z_X=\frac{x-{\mu }_X}{{\sigma }_X}$.
   したがって

$$Z_Y\mid X=x\sim \mathcal{N}(\rho \frac{x-{\mu }_X}{{\sigma }_X},1-{\rho }^2)$$

4. $Y$ の変換
   $Y={\mu }_Y+{\sigma }_Y{Z}_Y$ なので，条件付き分布は

$$Y\mid X=x\sim \mathcal{N}({\mu }_Y+\rho \frac{{\sigma }_Y}{{\sigma }_X}(x-{\mu }_X),{\sigma }_Y^2(1-{\rho }^2))$$

以上で導出完了.

---

参考文献

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る