相関係数の性質まとめ

解説

相関係数とは二つ以上の確率変数の間にある関係の強弱を表す指標で、$-1\le \rho \le 1$ を満たします.

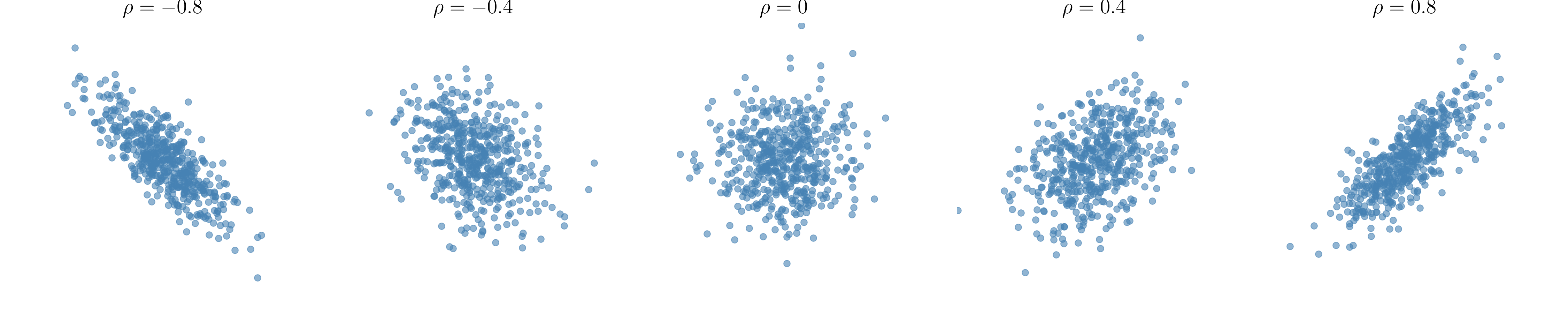
1に近づけば正の相関があるといい、確率変数 $X$ が増えれば $Y$ も増える関係にあります.

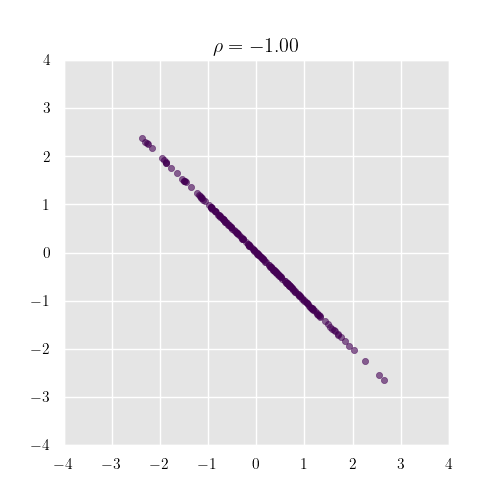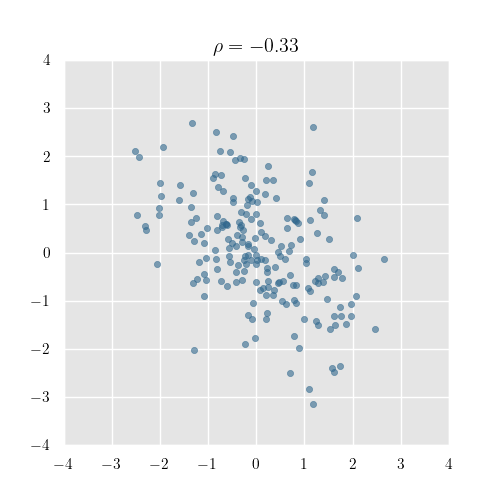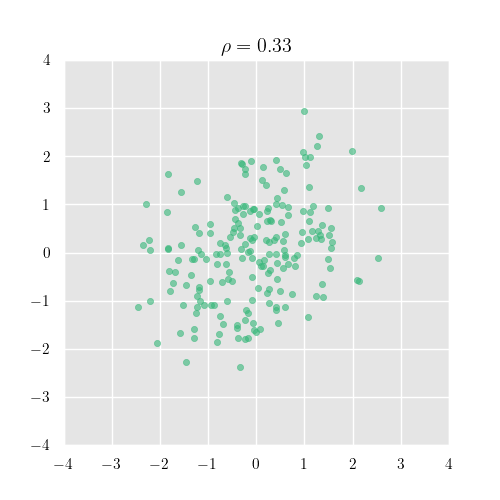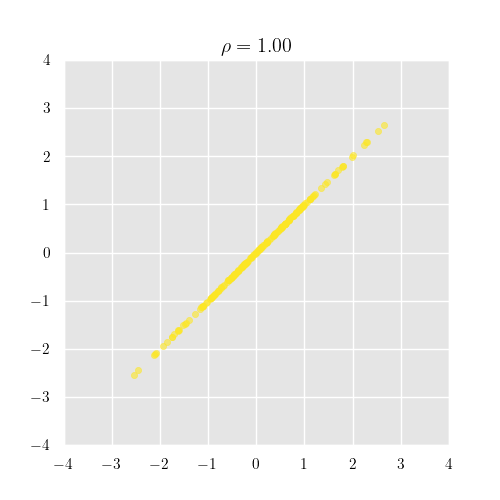
逆に-1に近ければ負の相関確率変数 $X$ が増えるとき $Y$ は減る関係にあります.[下図参照]

相関係数と言われればピアソンの積率相関係数を表すのが一般的です.

相関係数の定義

定義

確率変数 $X,Y$ のピアソンの積率相関係数は次で定義されます.

$${\rho }_{X,Y}=\frac{\mathrm{Cov}[X,Y]}{\sqrt{\mathrm{V}[X]}\sqrt{\mathrm{V}[Y]}}$$

ここで，

• $\mathrm{Cov}[X,Y]$ は共分散
• $\mathrm{V}[X],\mathrm{V}[Y]$ は分散

を表します.

---

性質

• $-1\le {\rho }_{X,Y}\le 1$

• ${\rho }_{X,Y}=0$ のとき $X,Y$ は無相関と呼ばれる
  （ただし独立とは限らない点に注意）

• 線形変換に対して不変
  $X^{\prime }=aX+b,Y^{\prime }=cY+d$ としても ${\rho }_{X^{\prime },Y^{\prime }}={\rho }_{X,Y}$ が成り立つ

• ${\rho }_{X,Y}=\pm 1$ のとき，$Y$ は $X$ の完全な線形関数

---

サンプル相関係数

定義

有限のデータ $(x_i,y_i)(i=1,\dots ,n)$ から計算する場合，標本相関係数は

$$r=\frac{\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum _{i=1}^n(x_i-\overline{x}{)}^2}\sqrt{\sum _{i=1}^n(y_i-\overline{y}{)}^2}}$$

で与えられます.

ここで $\overline{x},\overline{y}$ は標本平均です.

例題

• 例題1: 線形結合
  (2013年統計数理問1 改)

$X\sim \mathrm{Uniform}(0,1)$ とし，$Y=1-X$ のとき，確率変数 $X,Y$ の相関係数を求めよ.

解答

解答

まず，$X$ の基本的な統計量は

$$\mathbb{E}[X]=\frac{1}{2},\mathrm{V}[X]=\frac{1}{12}$$

です.

次に $Y=1-X$ なので，

$$\mathbb{E}[Y]=1-\mathbb{E}[X]=\frac{1}{2},\mathrm{V}[Y]=\mathrm{V}[1-X]=\mathrm{V}[X]=\frac{1}{12}$$

となります.

共分散は

$$\begin{array}{rl}\mathrm{Cov}[X,Y]& =\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y]\\ & =\mathbb{E}[X(1-X)]-\frac{1}{2}\cdot \frac{1}{2}\\ & =\mathbb{E}[X-X^2]-\frac{1}{4}\end{array}$$

ここで

$$\mathbb{E}[X]=\frac{1}{2},\mathbb{E}[X^2]=\frac{1}{3}$$

だから

$$\begin{array}{rl}\mathbb{E}[X-X^2]& =\frac{1}{2}-\frac{1}{3}=\frac{1}{6},\\ \mathrm{Cov}[X,Y]& =\frac{1}{6}-\frac{1}{4}=-\frac{1}{12}\end{array}$$

したがって，相関係数は

$$\begin{array}{rl}{\rho }_{X,Y}& =\frac{\mathrm{Cov}[X,Y]}{\sqrt{\mathrm{V}[X]}\sqrt{\mathrm{V}[Y]}}\\ & =\frac{-\frac{1}{12}}{\sqrt{\frac{1}{12}}\cdot \sqrt{\frac{1}{12}}}\\ & =\frac{-\frac{1}{12}}{\frac{1}{12}}\\ & =-1\end{array}$$

よって，$X,Y$ は完全な負の相関を持つ.

別解

共分散の線形性を使うとより簡単に計算できます.

$$\begin{array}{rl}\mathrm{Cov}[X,Y]& =\mathrm{Cov}[X,1-X]\\ & =\mathrm{Cov}[X,1]+\mathrm{Cov}[X,-X]\\ & =0-\mathrm{V}[X]\\ & =-\frac{1}{12}\end{array}$$

よって相関係数は

$$\begin{array}{r}{\rho }_{X,Y}=\frac{\mathrm{Cov}[X,Y]}{\sqrt{\mathrm{V}[X]}\sqrt{\mathrm{V}[Y]}}=\frac{-\frac{1}{12}}{\frac{1}{12}}=-1\end{array}$$

計算量が一気に減り，線形性を使うのが有効であることが分かります.

参考文献

新装改訂版　現代数理統計学

竹村 彰通

統計検定1級対策に定番の書籍 難易度は高めだが演習問題も豊富

Amazonで見る 楽天で見る